資源簡介

安徽省蕪湖市第一中學2024-2025學年高一下學期期中考試數學試卷
一、單選題
1．歐拉公式（其中i為虛數單位，），是由瑞士著名數學家歐拉創立的，公式將指數函數的定義域擴大到復數，建立了三角函數與指數函數的關聯，在復變函數論里面占有非常重要的地位，被譽為數學中的天橋．依據歐拉公式，的共軛復數為（ ）．
A． B． C． D．
2．設m，n是不同的直線，是不同的平面，則下列命題正確的是（ ）
A．若，則 B．若，則
C．若，則 D．若，則
3．如圖，在中，，點是的中點．設，，則（ ）

A． B． C． D．
4．如圖，水平放置的四邊形的斜二測直觀圖為矩形，已知，，則四邊形的周長為（ ）
A． B． C．8 D．10
5．在正方體中，E，F分別是線段，的中點，則異面直線，EF所成角余弦值是（ ）
A． B． C． D．
6．如圖，正三棱臺的下底面邊長為12，上底面邊長和側棱長均為6，則棱臺的體積為（ ）
A． B． C． D．
7．在中，內角的對邊分別為，若，則的形狀為（ ）
A．等腰三角形 B．直角三角形
C．等腰直角三角形 D．直角三角形或等腰三角形
8．如圖所示，在棱長為1的正方體中，點分別是棱的中點，是側面內一點，若平面，則線段長度的取值范圍是（ ）
A． B． C． D．
二、多選題
9．已知是復數且對應的點分別為，則以下結論錯誤的是（）．
A．若，則，且
B．若，則，且
C．若，則向量和相等或相反向量
D．若，則
10．的內角A、B、C的對邊分別為a、b、c，則下列說法正確的是（ ）
A．若，則 B．若，則是鈍角三角形
C．若，則為等腰三角形 D．若，則有兩解
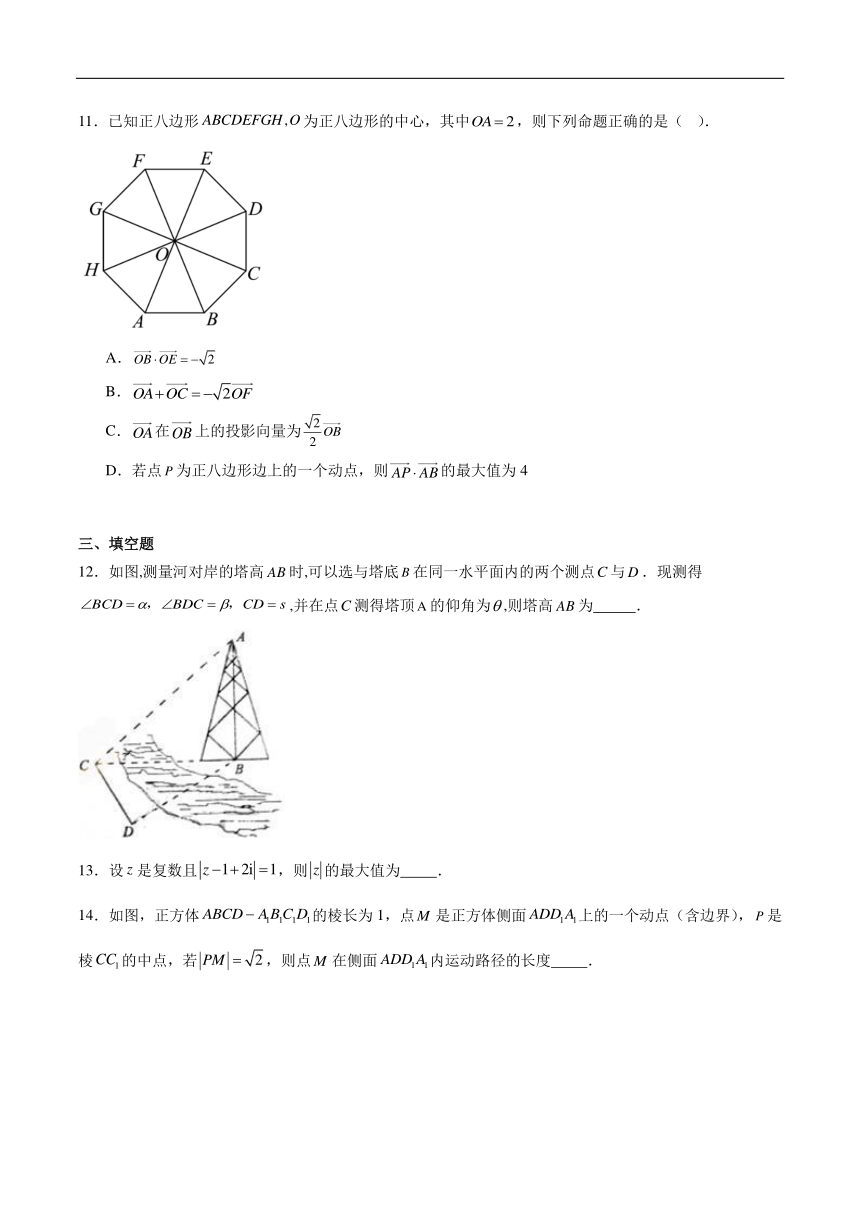
11．已知正八邊形為正八邊形的中心，其中，則下列命題正確的是（ ）．
A．
B．
C．在上的投影向量為
D．若點為正八邊形邊上的一個動點，則的最大值為4
三、填空題
12．如圖,測量河對岸的塔高時,可以選與塔底在同一水平面內的兩個測點與．現測得,并在點測得塔頂的仰角為,則塔高為 ．
13．設是復數且，則的最大值為 ．
14．如圖，正方體的棱長為1，點是正方體側面上的一個動點（含邊界），是棱的中點，若，則點在側面內運動路徑的長度 ．

四、解答題
15．已知向量.
(1)若向量與共線，求實數的值；
(2)若向量與的夾角為銳角，求實數的取值范圍.
16．在中，內角，，的對邊分別為，，，且．
(1)求；
(2)若的重心為，且，求．
17．如圖，在四棱錐中，底面為平行四邊形，為上的點，且，為中點．
(1)證明：平面；
(2)過F點作平面平面交于點，交于點，
（ⅰ）證明：；
（ⅱ）求的值．
18．如圖，在中，已知，點為邊的中點，相交于點．
(1)求；
(2)求；
(3)求．
19．在中，內角的對邊分別是，，．
(1)求角；
(2)若，求邊上的角平分線長；
(3)若為銳角三角形，求邊上的中線的取值范圍．
題號 1 2 3 4 5 6 7 8 9 10
答案 A D A D C C D B AC AD
題號 11
答案 BCD
1．A
根據歐拉公式及共軛復數的定義即可求解.
【詳解】，
所以的共軛復數為.
故選：.
2．D
利用線面位置關系，逐項判斷即得.
【詳解】對于A，，則或，A錯誤；
對于B，，則或，B錯誤；
對于C，，則直線可能相交，可能平行，也可能是異面直線，C錯誤；
對于D，由線面平行的性質知，D正確.
故選：D
3．A
根據向量的線性運算即可求得答案.
【詳解】由題意在中，，點是的中點，
故
，
故選：A
4．D
根據斜二測畫法的原則進行求解即可.
【詳解】由題設知：原四邊形中且，
所以原四邊形為平行四邊形，
而，則原四邊形中，故，
綜上，四邊形的周長為.
故選：D
5．C
如圖所示，連接，確定或其補角是異面直線EF與所成角，在直角中，計算得到答案.
【詳解】如圖所示：F是線段的中點，連接交于F，
由正方體的性質知，知異面直線，EF所成角即為直線，EF所成角，
故或其補角是異面直線EF與所成角.
設正方體邊長為2，在直角中，，，
故
故選：C
6．C
求出正三棱臺的高，再根據棱臺的體積公式即可求解.
【詳解】設上下底面的外心分別為，過作底面的垂線交于點，
上、下底面三角形的高分別為，，
所以，，
所以，又，
所以正三棱臺的高為，
上底面積為，下底面積為，
所以正三棱臺的體積為.
故選：.
7．D
將已知結合二倍角公式，兩角和的正弦公式，化簡可得，從而可以判斷三角形的形狀.
【詳解】，，
，
化簡得，，
，即，
或，
，或，即或，
是直角三角形或等腰三角形.
故選：D.
8．B
根據線面平行的條件構造面面平行從而得到點的軌跡，在根據平面幾何知識求出的范圍.
【詳解】如圖，取的中點，的中點，連接，顯然，且，
所以四邊形為平行四邊形，所以，又因為平面，
平面,所以平面，因為，平面，
平面,所以平面，又因為，所以平面平面，
因為平面，所以平面，點在側面上，所以點位于線段上，
因為，
，所以當點位于點時，最大，
當點位于的中點時，最小，
此時，
所以，所以線段長度的取值范圍是.
故選：B
9．AC
舉反例即可說明A，C錯誤；對于B，只有，才有；對于D，只有，才有，由比判斷D.
【詳解】對于A，若，，則滿足，但此時，故A錯誤；
對于B，，若，則故B正確；
對于C，若，則滿足，此時，
同理，此時和即不是相等何量，也不是相反向量，故C錯洖；
對于D，故，此時，故，故D正確.
故選：AC．
10．AD
利用大角對大邊及正弦定理，結合余弦定理即可求解.
【詳解】對于A，，所以，由正弦定理得，故A正確；
對于B，，故邊最長，角最大.
設，
則.
所以角為銳角，故是銳角三角形，故B錯誤；
對于C，，則或，即或，則為直角三角形或等腰三角形，故C錯誤；
對于D，，
根據正弦定理
，所以有兩解，所以有兩解，故D正確.
故選：AD.
11．BCD
根據題意，正八邊形的每條邊所對的角均為，且中心到各個頂點的距離都是，由向量的數量積的運算公式，可得判定A錯誤；連接交于點，得到，集合向量的線性運算法則，可得判定B正確；根據投影向量的計算方法，可判定C正確；設向量與的夾角為，得到，由，得到點在線段上運動時，取得最大值，利用向量的數量積的運算法則，結合正弦的倍角公式，可判定D正確.
【詳解】由題意知，正八邊形的每條邊所對的中心角均為，且中心到各個頂點的距離都是，
對于A中，由，所以A錯誤；
對于B中，連接交于點，則為的中點，且，
由，所以B正確；
對于C中，向量在上的投影向量為，
所以C正確；
對于D中，設向量與的夾角為，則，
其中表示在方向上的投影，
在正八邊形中，可得，延長交與點，
當點在線段上運動時，向量在方向上的投影取得最大值，
又由為等腰直角三角形，且，
在直角中，，
在等腰中，，
則，所以D正確.
故選：BCD.
12．
【詳解】試題分析：在中，，由正弦定理得，所以．在中，．
考點：1、正弦定理；2、三角形中的邊角關系．
13．/
根據復數模的幾何意義，結合圖象，即可求解.
【詳解】根據復數模的幾何意義可知，表示復平面內以為圓心，1為半徑的圓，而表示復數到原點的距離.
由圖可知，.
故答案為：.
14．/
確定點M在側面內的運動軌跡是圓弧，再求弧長即可.
【詳解】取中點E，連EM，PE，如圖，因是正方體的棱中點，

則PE//CD，而CD⊥平面，則有面，平面，
于是得PE⊥EM，由，PE=1得，EM=1，
因此，點M在側面內運動路徑是以E為圓心，1為半徑的圓在正方形內的圓弧，
如圖，圓弧所對圓心角為，圓弧長為.

故答案為：
15．(1)
(2)
（1）利用向量共線的坐標運算可知，即可求出參數值；
（2）利用兩向量夾角為銳角的充要條件是且與不共線，從而可得不等式組求解即可.
【詳解】（1）由題意可得，，
若向量與共線，可得，
解得.
（2）若向量與的夾角為銳角可得且與不共線，
即可得，
解得且，
即實數的取值范圍為且
16．(1)
(2)
（1）根據正弦定理邊角互化，再結合和差公式及二倍角公式即可求解;
（2）根據重心的性質可得，所以，兩邊平方后結合余弦定理可得，最后由正弦定理化簡可得答案.
【詳解】（1）因為，
所以，
化簡得，，，
即，
由解得或（舍去），
，．
（2）記中邊上的中線長為，由重心的性質得，
所以，
即，
等式兩邊平方可得，
所以，
又由余弦定理得，
所以，
整理得，解得，
由正弦定理得．
17．(1)證明見詳解
(2)（i）證明見詳解；（ii）
（1）連接交于，由三角形中位線可證，進而由線面平行的判定定理可證；
（2）（i）由面面平行的性質定理可證；（ii）猜測點H為靠近點P的三等點，在此基礎上證明平面平面即可.
【詳解】（1）連交于，因為底面為平行四邊形，
所以為的中點，而為的中點，所以，
又平面平面；
所以平面；
（2）（i）因為平面平面，平面平面，平面平面，
由面面平行的性質定理可得；
（ii）當為的三等點且時，有平面平面，下面證明：
因為為上的點，且，所以在中，，所以，
由（1）知平面，因為平面，所以平面，
由（i）可知，因為平面，平面，所以平面，
因為，所以平面平面，所以.
18．(1)
(2)
(3)
（1）根據和已知條件，兩邊平方，利用向量的運算求得的長，然后根據向量關系求得；
（2）建立直角坐標系，求出點的坐標，利用向量的夾角的坐標運算公式求；
（3）根據三點共線得，通過向量線性運算，將用和表示，從而將表示成，最后利用共線向量定理得到，求出的值再根據模長和數量積的運算可得.
【詳解】（1），
∴，又∵，∴，∴．
（2）如圖，以為原點，直線為軸建立直角坐標系.
依題得到：，，，，
設點，由可得：，
即，解得：，所以，
，，
則，，
由．
（3）三點共線，所以存在使得，，
，
，
又三點共線，所以，即．
，
所以
.
19．(1)
(2)
(3)
【詳解】（1）在中，由正弦定理及，
得
，
即，而，，
解得，又，所以.
（2）由及，余弦定理得，
又，解得，
由得，
即，則，所以.
（3）因為是的中點，所以，
則，
由正弦定理得，
即，
為銳角三角形， ，所以，所以，
所以，所以，
所以，
所以，即邊上的中線的取值范圍為．

展開更多......

收起↑