資源簡介

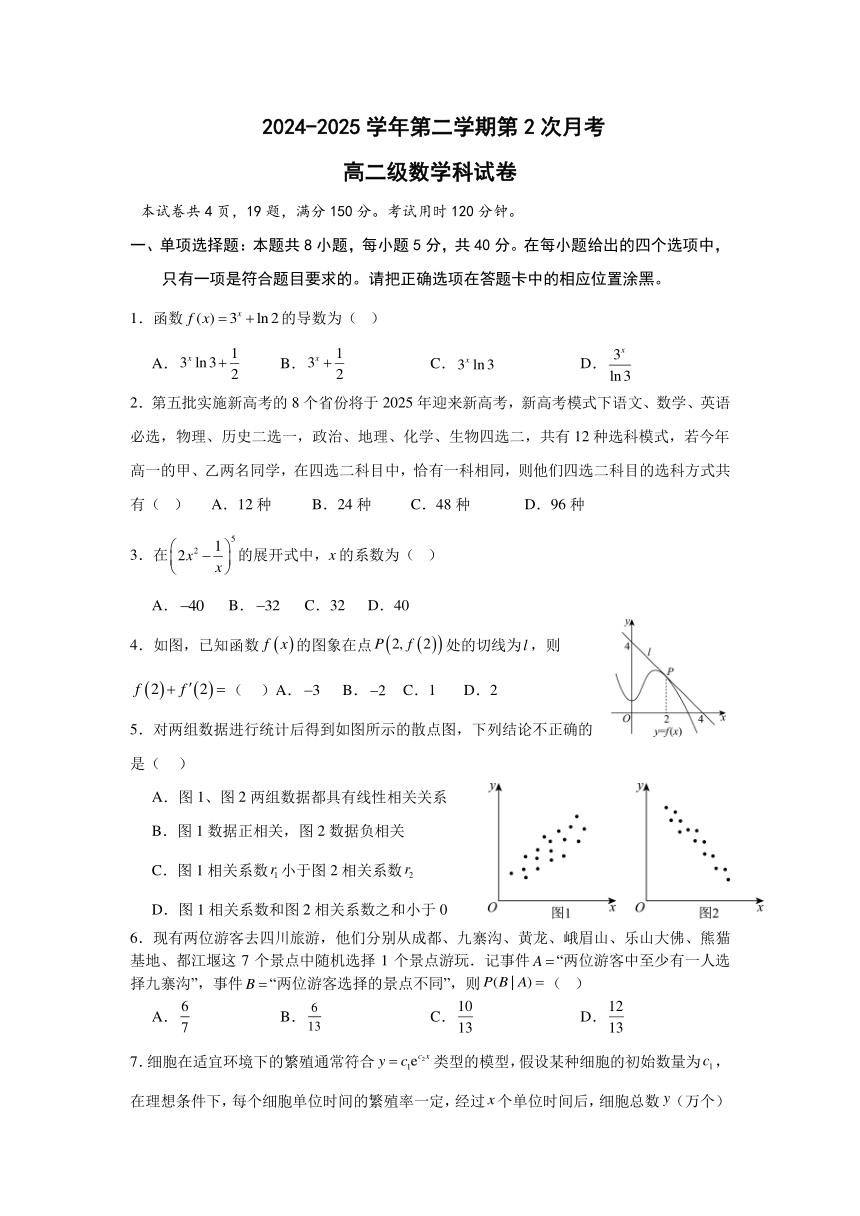
2024-2025學年第二學期第2次月考
高二級數學科試卷
本試卷共4頁，19題，滿分150分。考試用時120分鐘。
一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。請把正確選項在答題卡中的相應位置涂黑。
1．函數的導數為（ ）
A． B． C． D．
2．第五批實施新高考的8個省份將于2025年迎來新高考，新高考模式下語文、數學、英語必選，物理、歷史二選一，政治、地理、化學、生物四選二，共有12種選科模式，若今年高一的甲、乙兩名同學，在四選二科目中，恰有一科相同，則他們四選二科目的選科方式共有（ ） A．12種 B．24種 C．48種 D．96種
3．在的展開式中，x的系數為（ ）
A． B． C．32 D．40
4．如圖，已知函數的圖象在點處的切線為，則（ ）A． B． C．1 D．2
5．對兩組數據進行統計后得到如圖所示的散點圖，下列結論不正確的是（ ）
A．圖1、圖2兩組數據都具有線性相關關系
B．圖1數據正相關，圖2數據負相關
C．圖1相關系數小于圖2相關系數
D．圖1相關系數和圖2相關系數之和小于0
6．現有兩位游客去四川旅游，他們分別從成都、九寨溝、黃龍、峨眉山、樂山大佛、熊貓基地、都江堰這7個景點中隨機選擇1個景點游玩．記事件“兩位游客中至少有一人選擇九寨溝”，事件“兩位游客選擇的景點不同”，則（ ）
A． B． C． D．
7．細胞在適宜環境下的繁殖通常符合類型的模型，假設某種細胞的初始數量為，在理想條件下，每個細胞單位時間的繁殖率一定，經過個單位時間后，細胞總數（萬個）會呈指數增長．設，變換后得到線性回歸方程，已知該回歸方程的樣本中心為，則（ ）
A． B．0.596 C． D．0.206
8．（2024·浙江溫州·一模）已知函數的值域為，則實數的取值范圍為（ ）
A． B． C． D．
二、多項選擇題：本題共3小題，每小題6分，共18分。在每小題給出的選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。
9．已知變量之間的線性回歸方程為，且變量之間的一組相關數據如表所示，則下列說法正確的是（ ）
x 6 8 10 12
y 6 m 3 2
A．變量之間呈現負相關關系 B．
C．可以預測，當時，y約為
D．由表格數據知，該回歸直線必過點
10．某種子站培育出A、B兩類種子，為了研究種子的發芽率，分別抽取 100粒種子進行試種，得到如下餅狀圖與柱狀圖：用頻率估計概率，且每一粒種子是否發芽均互不影響，則（ ）
A．若規定種子發芽時間越短，越適合種植，則從5天內的發芽率來看，B類種子更適合種植
B．若種下12粒A類種子，則有10粒種子5天內發芽的概率最大
C．從樣本A、B兩類種子中各隨機取一粒，則這兩粒種子至少有一粒8天內未發芽的概率是0.145
D．若種下10粒B類種子， 5至8天發芽的種子數記為X， 則
11．中國南北朝時期的著作《孫子算經》中，對同余除法有較深的研究.設a，b，m（）為整數，若a和b被m除得的余數相同，則稱a和b對模m同余，記為.若，，則b的值不可能的是（ ）
A．2018 B．2020 C．2022 D．2024
三、填空題：本題共3小題，每小題5分，共15分。請把答案填在答題卡的相應位置上。
12．已知隨機變量，，則 .
13．三部機器生產同樣的零件，其中機器甲生產的占40%，機器乙生產的占25%，機器丙生產的占35%．已知機器甲、乙、丙生產的零件分別有3%、5%和1%不合格．三部機器生產的零件混合堆放在一起，現從中隨機地抽取一個零件．則取到的是不合格品的概率是 ．（答案用小數作答）
14．已知方程有兩個解，則實數m的取值范圍為 .
四、解答題：本題共5小題，共77分。解答應寫出文字說明、證明過程或演算步驟。
15．（13分）已知在二項式的展開式中，前三項系數的和是97．
(1)求的值； (2)求展開式中二項式系數最大的項；
(3)求展開式中所有的有理項．
16．（15分）已知函數（）．
(1)若是函數的極值點，求a的值；(2)討論的單調性．
17．（15分）某公園為了提升公園形象，提高游客旅游的體驗感，他們更新了部分設施，調整了部分旅游線路.為了解游客對新措施是否滿意，隨機抽取了100名游客進行調查，男游客與女游客的人數之比為2:3，其中男游客有35名滿意，女游客有15名不滿意.
滿意 不滿意 總計
男游客 35
女游客 15
合計 100
(1)完成列聯表，依據表中數據，以及小概率值的獨立性檢驗，能否認為游客對公園新措施滿意與否與性別有關
(2)從被調查的游客中按男、女分層抽樣抽取5名游客.再隨機從這5名游客中抽取3名游客征求他們對公園進一步提高服務質量的建議，其中抽取男游客的人數為.求出的分布列及數學期望.
參考公式：，其中.
參考數據：
0.10 0.05 0.010 0.005
2.706 3.841 6.635 7.879
18．（17分）“綠色出行，低碳環保”的理念已經深入人心，逐漸成為新的時尚.甲、乙、丙三人為響應“綠色出行，低碳環保”號召，他們計劃每天選擇“共享單車”或“地鐵”兩種出行方式中的一種.他們之間的出行互不影響，其中，甲每天選擇“共享單車”的概率為，乙每天選擇“共享單車”的概率為，丙在每月第一天選擇“共享單車”的概率為，從第二天起，若前一天選擇“共享單車”，后一天繼續選擇“共享單車”的概率為，若前一天選擇“地鐵”，后一天繼續選擇“地鐵”的概率為，如此往復.
(1)若3月1日有兩人選擇“共享單車”出行，求丙選擇“共享單車”的概率；
(2)求丙在3月2日選擇“共享單車”的概率；
(3)記甲、乙、丙三人中3月1日選擇“共享單車”出行的人數為，求的分布列與數學期望.
19．（17分）已知函數.
(1)當時，求曲線在點處的切線方程；
(2)若有兩個極值點，求的取值范圍；
(3)在（2）的條件下，證明：當時，.
2024-2025學年第二學期第2次月考
高二級數學科答案
1．C 2．B 3．A 4．C 5．C
6．D【詳解】事件的對立事件為： “兩位游客無人人選擇九寨溝”，所以，
又，所以.故選：D
7【答案】A【詳解】由題意得，解得，
因此，由兩邊取對數，得，
又，所以，即．故選：A．
8【答案】A【詳解】當時，的取值范圍是，
注意到，則，
當時，，當時，，
所以在上單調遞增，在上單調遞減，
所以當時，的最大值為，
且注意到趨于負無窮時，也會趨于負無窮，
若函數的值域為，
則當且僅當，解得.故選：A.
9【答案】ABD【詳解】對于A，由得：，故呈負相關關系，A正確；對于B，，，
，解得：，B正確；對于C，當時，，C錯誤；對于D，由知：，回歸直線必過點，即必過點，D正確.
10【答案】BC【詳解】從5天內的發芽率來看，A類種子為，B類種子為，故A錯誤；若種下12粒A類種子，由題意可知發芽數X服從二項分布，，
，
則，且，
可得，且，
所以，即，即有10粒種子5天內發芽的概率最大，故B正確；
記事件A: 樣本A種子中隨機取一粒8天內發芽；
事件B: 樣本B種子中隨機取一粒8天內發芽；
根據對立事件的性質，這兩粒種子至少有一粒8天內未發芽的概率：
，故C正確；
由題意可知X服從二項分布，，
所以，故D錯誤；故選：BC
11【答案】ACD【詳解】由，得
，
所以，
即被除得的余數為，結合選項可知只有被除得的余數為，即b的值不可能的是ACD.故選：ACD
12.0.7【詳解】由題意得，所以.
13.0.028【詳解】根據題意得，取到的是不合格品的概率是
.
14.【詳解】若有兩個零點，則有兩個解，
等價于有兩個解，因為，，所以，
令，原式等價于有兩個解，
因為，則當時，所以在上單調遞增，
所以有兩個大于零的解.
解，可得，令，
則，當時，，當時，，
所以在上單調遞增，在上單調遞減，且，的圖象如圖：
所以當時，有兩個交點，即有兩個零點.
15.【詳解】（1）解：由二項式展開式的通項為，
可得展開式的前3項的系數分別為，
因為前3項的系數和為，可得，且，
解得或（舍去），即的值為.
（2）解：由，
當時，二項式系數最大，即二項式系數最大項為．
（3）解：由，可得，
所以展開式的有理項為．
16.【詳解】（1）由題意可得的定義域為，且，
∵是函數的極值點，∴，即．
當時，，由得，
當時，，單調遞增，當時，，單調遞減；
∴滿足是函數的極值點，因此.
（2），
當時，因為，所以，則，在上單調遞增；
當時，得，
當時，，單調遞增；當時，，單調遞減；
則函數的單調增區間為，單調減區間為；
綜上可知：當時，的單調增區間為，無單調減區間；
當時，函數的單調增區間為，單調減區間為.
17.【詳解】（1）因為調查的男游客人數為：，所以，調查的女游客人數為，于是可完成列聯表如下：
滿意 不滿意 總計
男游客 35 5 40
女游客 45 15 60
合計 80 20 100
零假設為：游客對公園新措施滿意與否與性別無關.根據列聯表中的數據，可得：
，
根據小概率值的獨立性檢驗，沒有充分證據推斷不成立，因此可以認為成立，即游客對公園新措施滿意與否與性別無關；
（2）由（1）可知男游客抽2人，女游客抽3人，依題意可知的可能取值為0，1，2，并且服從超幾何分布，即，，.
所以的分布列為：
0 1 2
.
18.【詳解】（1）記甲、乙、丙三人3月1日選擇“共享單車”出行分別為事件，
記三人中恰有兩人選擇“共享單車”出行為事件，
則，
又，
所以，
即若3月1日有兩人選擇“共享單車”出行，丙選擇“共享單車”的概率為.
（2）設丙在3月第n天選擇“共享單車”的概率為
由題意得，則.
（3）依題意，的所有可能取值為0，1，2，3，
則，
，
，，
所以的分布列為
0 1 2 3
數學期望.
19.【詳解】（1）當時，，所以，
所以，所以曲線在點處的切線斜率，
所以曲線在點處的切線方程為，即.
（2）函數的定義域為，
因為有兩個極值點，
意味著有兩個不同的變號正根.
設，，則.
若，，在上單調遞增，不會有兩個正根；
當，令，得，
所以當時，所以在上單調遞增；
當時，所以在上單調遞減.
又當時，當時，
要使有兩個正根，需，即，解得.
所以當時，有兩個極值點.
（3）的定義域為，
因為有兩個極值點，意味著是有兩個不同正根.
所以，且，
所以，所以，
所以，當時，
，
令，即證當時，對恒成立.
令，則.
因為，所以，所以，
所以在上單調遞增，所以，即，
所以當時，恒成立.試卷第1頁，共3頁
答案第1頁，共2頁

展開更多......

收起↑