資源簡介

旺蒼縣2025年春九年級第三次診斷性測試數學試卷
說 明： 1.全卷滿分150分，考試時間120分鐘。
2.本試卷分為第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分，共三個大題26個小題。
第Ⅰ卷 選擇題(共30分)
一、選擇題(每小題給出的四個選項中，只有一個符合題意.每小題3分，共30分)
的倒數是 ( )
A. C.4 D. -4
2.下列計算正確的是 ( )
3.在平面直角坐標系中，點M的坐標為(-3，2)，則點 M關于原點對稱的點的坐標為 ( )
A.(-2,-3) B.(2,3)
C.(2,-3) D.(3,-2)
4.某校合唱團共有50名成員，她們的年齡分布如下表：
年齡/歲 12 13 14 15
人數 5 24
由于表格污損，14歲、15歲的人數看不清，則下列關于年齡的統計量可以確定的是 ( )
A.平均數、眾數 B.眾數、中位數
C.平均數、中位數 D.中位數、方差
5.如圖,在等邊三角形ABC中,BD⊥AC,垂足為點 D,AB的垂直平分線交AB 于點 E,交BD于點F,若BC=6,則EF的長為 ( )
A.3 B. C.2 D.1.5
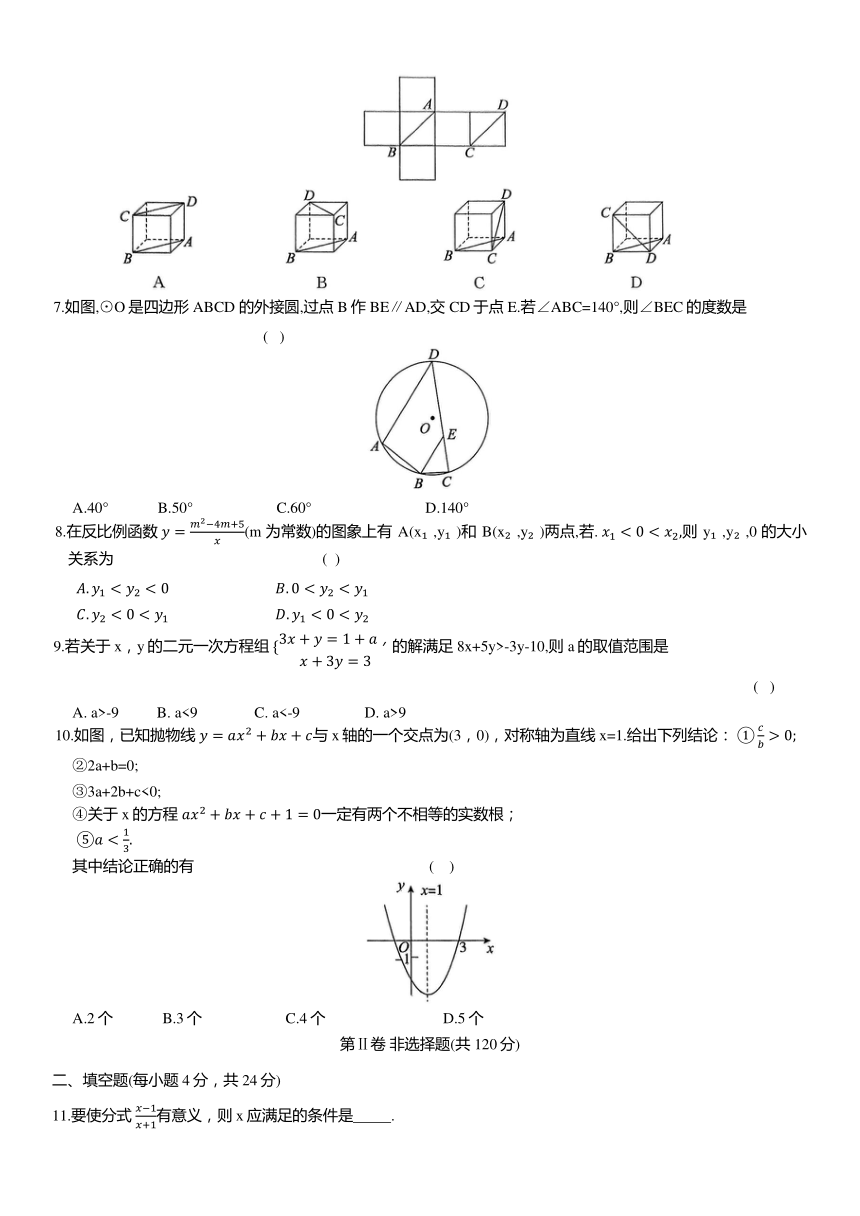
6.若將如圖所示的平面圖形圍成正方體，則這個正方體可以是 ( )
7.如圖,⊙O是四邊形ABCD 的外接圓,過點 B作BE∥AD,交CD于點 E.若∠ABC=140°,則∠BEC的度數是 ( )
A.40° B.50° C.60° D.140°
8.在反比例函數 (m為常數)的圖象上有 A(x ,y )和B(x ,y )兩點,若. 則y ,y ,0的大小關系為 ( )
9.若關于x，y的二元一次方程組 的解滿足8x+5y>-3y-10,則a的取值范圍是
( )
A. a>-9 B. a<9 C. a<-9 D. a>9
10.如圖，已知拋物線 與x軸的一個交點為(3，0)，對稱軸為直線x=1.給出下列結論：
②2a+b=0;
③3a+2b+c<0;
④關于x的方程 一定有兩個不相等的實數根；
其中結論正確的有 ( )
A.2個 B.3個 C.4個 D.5個
第Ⅱ卷 非選擇題(共120分)
二、填空題(每小題4分，共24分)
11.要使分式 有意義，則x應滿足的條件是 .
12.唐家河國家級自然保護區是以大熊貓及其棲息地為主要保護對象的自然保護區，總面積4萬公頃，2021年9月30日經國務院批復成立大熊貓國家公園.已知1公頃=10000平方米，則該自然保護區的總面積用科學記數法表示為 平方米.
13.如圖,在△ABC中,在邊AB,BC,CA上分別取點C ,A ,B ,使得 點A 是邊BC上任意一點，連接三點得到△A B C .重復上面過程，在△A B C 的邊 上分別取點 C ,A ,B ,使得 點 A 是邊 B C 上任意一點，連接三點得到△A B C ,按此方式繼續重復操作,直到得到△A B C .設△ABC的面積為1,則 的面積為 .
14.已知二次函數 的圖象向左平移1個單位長度，再向下平移2個單位長度得到拋物線C,點 M(-3,y ),N(2,y )在拋物線C上,則 y y (填“>”“<”或“=”).
15.如圖,在 Rt△ABC中, 點 P 為邊 AC上的動點,連接BP,過點 A作, 交 BP 的延長線于點 M.當點 P 從點 A 運動到點 C時，線段 BM的中點 N 運動的路徑長為 .
16.如圖，在正方形紙片ABCD中，點E是邊AB 的中點，將正方形紙片沿EC折疊，點 B落在點P 處，延長CP交AD 于點Q,連接AP并延長,交CD于點F.給出以下結論:①AQ=PQ;②點F為CD的中點;③CF =PC·PQ;④cos∠DCQ= 其中結論正確的是 (填序號).
三、解答題(要求寫出必要的解答步驟或證明過程，共96分)
17.(6分)
計算：
18.(8分)
先化簡，再求值：若 求代數式 的值.
19.(8分)
如圖，在矩形ABCD中，
(1)尺規作圖：請用無刻度的直尺和圓規作線段BD的垂直平分線.
(要求：不寫作法，保留作圖痕跡，并把作圖痕跡用黑色簽字筆描黑)
(2)在(1)的條件下，線段BD的垂直平分線分別交CD，AB于M，N兩點，求MN的長.
20.(9分)
為更好地提升服務質量，某旅行社隨機調查了部分游客對“昭化肥腸、太守麻花、宮保雞丁、火鍋魚”四種美食的喜好情況(每人限選一種)，并將調查結果繪制成不完整的統計圖，如圖所示.根據圖中信息，解答下列問題.
(1)本次抽取游客 人，扇形統計圖中m的值為 .
(2)請補全條形統計圖.
(3)該旅行社推出每人可免費品嘗兩種美食的活動，某游客從上述四種美食中隨機選擇兩種，請用畫樹狀圖或列表的方法求選到“昭化肥腸和火鍋魚”的概率.
21.(9分)
如圖，點A 是“某紀念碑”頂部一點，AB的長表示點A 到水平地面的距離.某測量小組在紀念碑前水平地面的點 M 處架起測量儀，將測量儀鏡頭調到距離地面1米的點C 處時，測得點 A 的仰角 然后將測量儀鏡頭再升高0.47米到點E 處，測得點 A 的仰角. 已知圖中各點均在同一豎直平面內，請根據上述數據，計算紀念碑頂部點A 到地面的距離AB 的長.
(結果精確到1米.參考數據：si ,
22.(10分)
某民宿有A，B兩種客房，其中A種客房12間，B種客房10間.若全部入住，一天的營業額為3600元；若A，B兩種客房均有5間入住，一天的營業額為1600元.
(1)A，B兩種客房每間的定價分別是多少元
(2)該民宿對一段時間內B種客房的入住情況進行調研后發現：如果客房不調價，房間可全部住滿；如果每間客房的定價每增加20元，就會有一間客房空閑.當B種客房每間的定價為多少元時，B種客房一天的營業額W 最大 最大營業額為多少元
23.(10分)
如圖，一次函數.y=ax+b的圖象與反比例函數 的圖象相交于A，B兩點，其中點 A 的坐標為(--2,m),點 B的坐標為(3,-2).
(1)求這兩個函數的解析式.
(2)根據圖象，直接寫出關于x的不等式 的解集.
(3)在x軸上作一點 P，使AP-PB的值最大，并求出點 P 的坐標.
24.(10分)
如圖，點A 在 的邊CD上,以AB為直徑的⊙O交 BC于點E,交BD于點F,連接AE,AF,EF,∠BAF=∠CDB.
(1)求證:直線CD是⊙O的切線.
(2)若⊙O的半徑 求EF的長.
25.(12分)
(1)已知 和 都是等腰直角三角形，
①如圖1，當點 D在線段BC 上時，連接CE，請探究 CE和BD 之間的數量關系，并說明理由；
②如圖2，當點 D在線段BC的延長線上時，連接CE，請再次探究CE和BD 之間的數量關系，并說明理由.
(2)如圖3，在等腰直角三角形ABC中， 點 P 在線段AC 上, 點 D 是BC 延長線上的動點，連接DP，以DP為腰在DP的右側作等腰直角三角形DPF， 連接CF.當 時,求 BD的長.
26.(14分)
如圖，二次函數 的圖象的頂點坐標為( 與y軸交于點C(0,3),與x軸分別交于點A 和點B(點A 在點B 左側)，P，Q為拋物線上的兩點.
(1)求該二次函數的解析式和A，B兩點的坐標.
(2)以AB為直徑作圓，圓心為( 求點C與 上的點的最短距離.
(3)設點 P 的橫坐標為m，點Q的橫坐標為 的面積S 是否存在最小值 若存在，請求出最小值；若不存在，請說明理由.
參考答案
一、選擇題(每小題3分，共30分)
題號 1 2 3 4 5
答案 C D D B B
題號 6 7 8 9 10
答案 B A D A C
二、填空題(每小題4分，共24分)
11. x≠-1 12.4×10 13.2- (或 ) 14.> 15.π/
16.①②③
三、解答題(共96分)
17.解:
·· ………… …… 2分
…… 4 分
=3. 6分
18.解:
2分
m … … 4分
6分
∴原式=2. 8分
19.解:(1)如圖,直線EF 即為所求, 3分
(2)如圖,連接DN,設MN與BD 交于點O.
∵在矩形ABCD中
5分
根據作圖過程可知，MN是BD的垂直平分線，
∴DN=BN,OB=OD=2
∴AN=AB--BN=AB--DN=8-DN.
在 Rt△ADN中，根據勾股定理，得
解得 DN=5. 6分
在 Rt△DON中，根據勾股定理，得
∵CD∥AB,
∴∠MDO=∠NBO,∠DMO=∠BNO.
又OD=OB,
∴△DMO≌△BNO(AAS).
8分
20.解:(1)240 35 2分
(2)喜好火鍋魚的人數為240-48-72-84=36,補全條形統計圖如下：
5分
(3)把四種美食分別記為A：昭化肥腸，B：太守麻花，C：宮保雞丁，D：火鍋魚.畫樹狀圖如下：
共有12種等可能出現的結果，其中選到“A和D”的結果有2種，
∴選到“昭化肥腸和火鍋魚”的概率為 ……9分
21.解:如圖,延長CD交AB于點H,延長EF交AB 于點 N.易得四邊形 CENH 為矩形,∴EN=CH.
設點 A 到地面的距離AB的長為h，
參考答案第1頁
由題意，得△ACH 和△AEN 均為直角三角形.在Rt△ACH中,∠AHC=90°,∠ACH=37.5°,
4分同理可得，
6分∵CH=EN,
解得h≈19.
答：紀念碑頂部點 A 到地面的距離AB 的長約為19米.
9分
22.解：(1)設A 種客房每間的定價是 x元，B種客房每間的定價是y元，
由題意，得 3 分解得
答：A，B兩種客房每間的定價分別是200 元、120 元.5分
(2)設B種客房每間的定價為 a 元，則
8分
∴當a=160時,W 取最大值,最大值為1280.
答：當B種客房每間的定價為160元時，B種客房一天的營業額W 最大，最大營業額為1280元. 10分
23.解:(1)∵一次函數y= ax+b的圖象與反比例函數 y=kx的圖象相交于A，B 兩點，其中點A 的坐標為(-2， m),點B的坐標為(3,-2),
∴k=-2×m=3×(-2).
∴k=-6,m=3.
∴反比例函數的解析式為 3分∵A(-2,3),B(3,-2)在一次函數 y= ax+b的圖象上, 解得
∴一次函數的解析式為y=-x+1. 5分
(2)由圖象可知，關于x的不等式 的解集為-23. 7分
(3)如圖，作點 B關于x軸的對稱點B'，連接AB'并延長交x軸于點 P，點P 即為所求.
∵B(3,-2),∴B'(3,2). 8分
易得直線 AB'的函數解析式為
令y=0,∴x=13.
∴點 P 的坐標為(13,0). 10分
24.(1)證明:∵AB 是⊙O的直徑,
∴∠AFB=90°.
∴∠BAF+∠ABD=90°.
∵∠BAF=∠CDB,∴∠CDB+∠ABD=90°.
∴∠BAD=90°,即AB⊥CD.
又AB是⊙O的直徑，
∴直線 CD是⊙O的切線. 4分
(2)解:在 Rt△ABD中,
∵AB=2r=8,AD=6,
5分
在 Rt△ABC中,
∵AB=8,AC=8,
6分
∵AB是⊙O的直徑,∴AE⊥BC.
7分
∵∠BEF=∠BAF,∠BAF=∠CDB,
∴∠BEF=∠CDB.
又∠EBF=∠DBC,∴△BEF∽△BDC.
即
解得 即EF的長為 10分
25.解:(1)①如圖1,過點E作EH⊥BC,交 BC的延長線于點H,由已知可得,∠ABD=∠DHE,AD=DE,
易證∠ADB=∠DEH,
∴△ABD≌△DHE(AAS).
∴BD=EH,AB=DH.
……… …………… 2分
∵AB=BC,
∴BC=DH.
∴BC-CD=DH-CD. 3分
∴BD=CH.
∴CH=EH.
∴△CEH 為等腰直角三角形.
4分
②如圖2,過點 E 作EG⊥BC,交 BC的延長線于點G,
由已知可得,∠ABD=∠DGE,AD=DE,
易證∠ADB=∠DEG,
∴△ABD≌△DGE(AAS).
∴BD=EG,AB=DG. 5分
∵AB=BC,
∴BC=DG.
∴BC+CD=DG+CD. 6分
∴BD=CG.
∴CG=EG.
∴△CEG 為等腰直角三角形.
8分
(2)如圖3,過點 P 作PM⊥BC于點M,過點 F 作FN⊥BC,交 BC的延長線于點 N,
易證△PMC為等腰直角三角形.
∴PM=MC=4. 9分
由(1)易知△PMD≌△DNF,
∴MD=FN,MP=DN.
∵MP=MC,
∴MC=DN.
∴MC+CD=DN+CD.
∴MD=CN.
∴CN=FN.
∴△CFN是等腰直角三角形.
∴∠FCN=45°.
又∠PCM=45°,
∴∠PCF=90°.
∴△PCF 為直角三角形. 11分
設CD=x,則
MD=4+x.
易得
又∠PFC=30°,
12分
26.解:(1)由題意,得 ,將C(0,3)代入,得a+4=3,∴a=-1.
∴該二次函數的解析式為 … … 2分把y=0代入，得 解得 ∴A(-3,0),B(1,0). 4分
(2)如圖1,連接CO ,
∵AB為⊙O 的直徑,A(-3,0),B(1,0),
∴O (-1,0),AB=4.
∴⊙O 的直徑為4,半徑為2. 6分
由勾股定理，得 7分
∴點 C 與⊙O 上的點的最短距離為 …… 9分
(3)存在. 10分
易得點 點 當直線 PQ∥x軸時,
易得
當直線 PQ與x軸不平行時， 如圖2，設直線PQ交x軸于點 H,
由點 P，Q的坐標，得直線 PQ 的函數解析式為 y=
令y=0,則
∴點 H 的坐標為
∴△OPQ的面積 12分
綜上所述，△OPQ的面積S 存在最小值，

展開更多......

收起↑