資源簡介

中小學教育資源及組卷應用平臺
數學人教版8年級上冊
第11單元（三角形） 單元專題卷
（時間：120分鐘 總分：120分）
學校:___________姓名：___________班級：___________學號：___________
題號 一 二 三 四 總分
得分
一、單選題（共15題 滿分45分 每題3分）
1．在中，，，則的度數為（　　）
A． B． C． D．
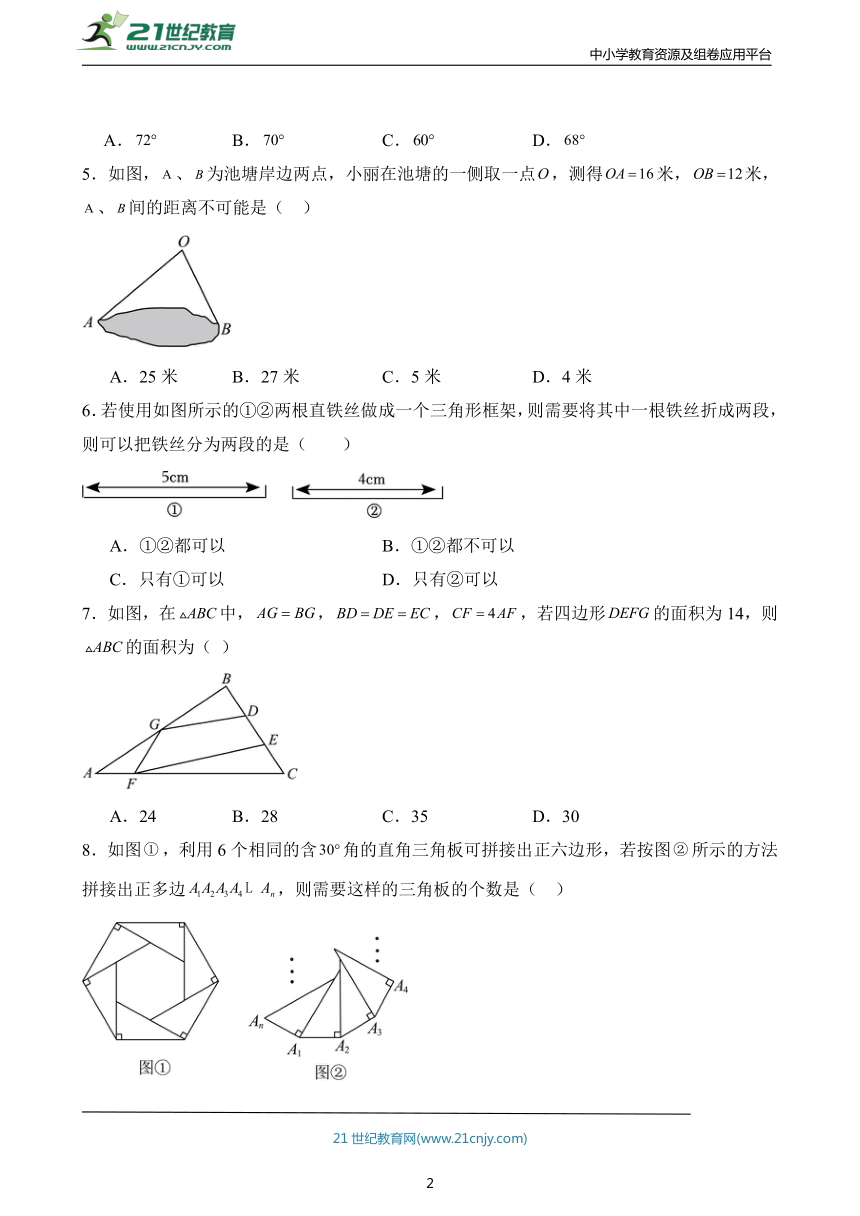
2．如圖，已知點是射線上一動點（不與點重合），，若是鈍角三角形，則的取值范圍是（ ）
A． B．
C．或 D．或
3．的三個角的關系為，則是（ ）
A．等邊三角形 B．以AC為斜邊的直角三角形
C．以為斜邊的直角三角形 D．不確定
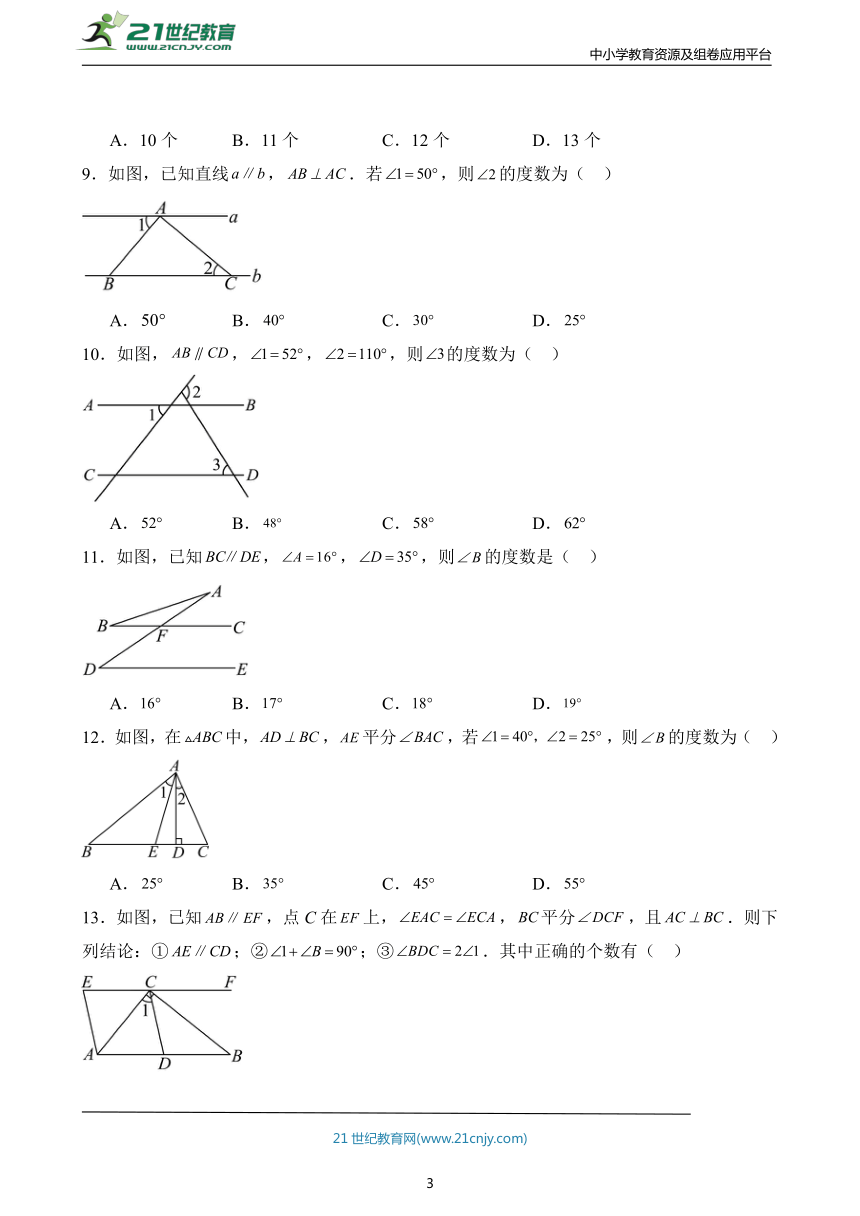
4．中國古典園林里面的窗型，形制豐富，如題圖是頤和園小長廊五角加膛窗，其輪廓是一個正五邊形，如題圖是它的示意圖，它的一個外角的度數為（ ）

A． B． C． D．
5．如圖，、為池塘岸邊兩點，小麗在池塘的一側取一點，測得米，米，、間的距離不可能是（ ）
A．25米 B．27米 C．5米 D．4米
6．若使用如圖所示的①②兩根直鐵絲做成一個三角形框架，則需要將其中一根鐵絲折成兩段，則可以把鐵絲分為兩段的是（　　）
A．①②都可以 B．①②都不可以
C．只有①可以 D．只有②可以
7．如圖，在中，，，，若四邊形的面積為14，則的面積為（ ）
A．24 B．28 C．35 D．30
8．如圖，利用6個相同的含角的直角三角板可拼接出正六邊形，若按圖所示的方法拼接出正多邊，則需要這樣的三角板的個數是（ ）
A．10個 B．11個 C．12個 D．13個
9．如圖，已知直線，．若，則的度數為（ ）
A． B． C． D．
10．如圖，，，，則的度數為（ ）
A． B． C． D．
11．如圖，已知，，，則的度數是（ ）

A． B． C． D．
12．如圖，在中，，平分，若，則的度數為（ ）
A． B． C． D．
13．如圖，已知，點C在上，，平分，且．則下列結論：①；②；③．其中正確的個數有（ ）
A．①② B．①③ C．②③ D．①②③
14．如圖是一款椅子的側面示意圖，已知與地面平行，，，則的度數是（ ）
A． B． C． D．
15．閱讀材料：各個角都相等且各條邊都相等的n邊形叫做正n邊形，例如正三邊形（即等邊三角形）、正四邊形（即正方形）．
如圖1，在正三邊形中，，
，
如圖2，在正四邊形中，，
；
如圖3，在正五邊形中，
，
，……，
依次下去，點在第n個圖中，的度數是（ ）
A． B． C． D．
二、填空題（共5題 滿分20分 每題4分）
16．如圖，已知， 垂足為點，，則等于 ．
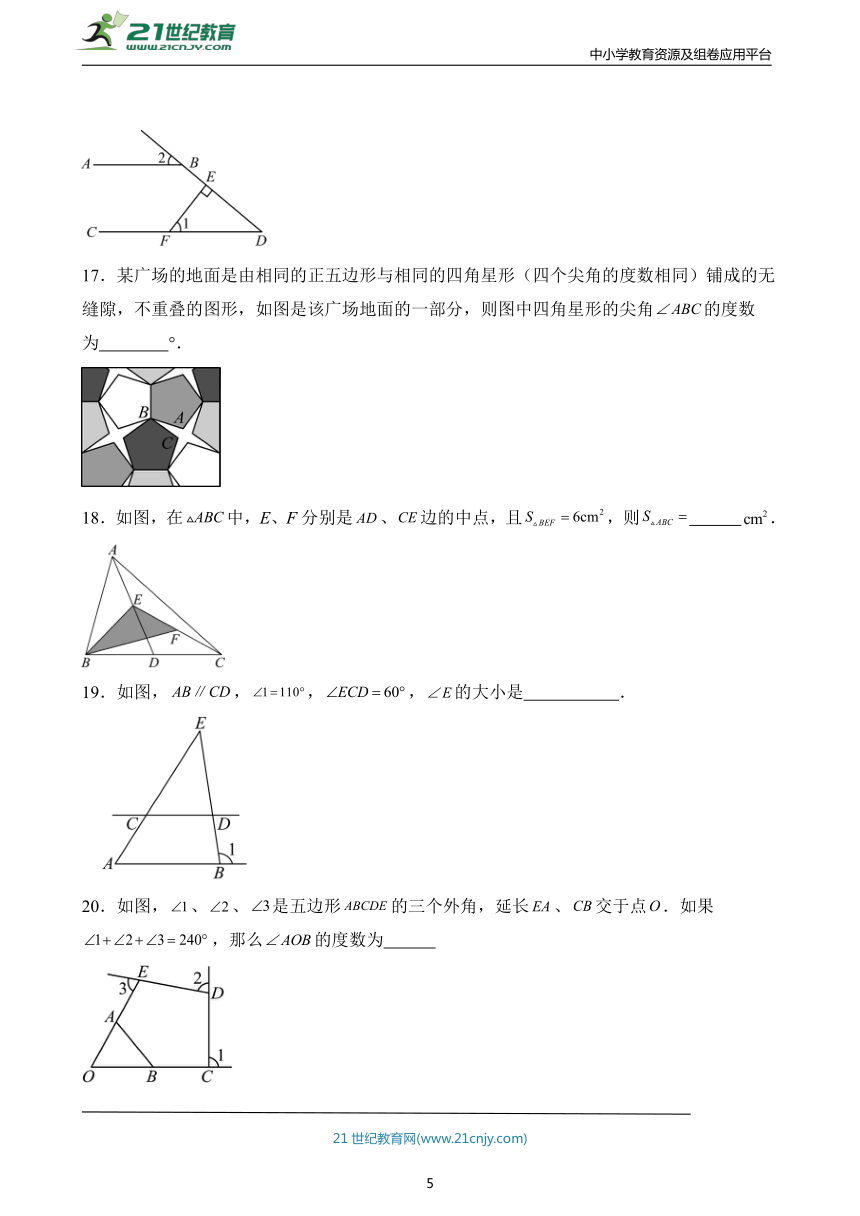
17．某廣場的地面是由相同的正五邊形與相同的四角星形（四個尖角的度數相同）鋪成的無縫隙，不重疊的圖形，如圖是該廣場地面的一部分，則圖中四角星形的尖角的度數為 °．
18．如圖，在中，E、F分別是、邊的中點，且，則 ．

19．如圖，，，，的大小是 ．
20．如圖，、、是五邊形的三個外角，延長、交于點．如果，那么的度數為
三、解答題（共6題 滿分55分）
（8分）21．兩根木棒的長分別是和．要選擇第三根木棒，將它們首尾相接釘成一個三角形．若第三根木棒的長為偶數，則第三根木棒長的取值情況有幾種
（8分）22．如圖，在中，AD是BC邊上的高，CE平分，若，，求的度數．
（9分）23．如圖，在中，∠B=25°，∠BAC=31°，過點A作BC邊上的高，交BC的延長線于點D，CE平分∠ACD，交AD于點E．求：（1）∠ACD的度數；（2）∠AEC的度數．
（10分）24．如圖，點E在上，點F在的延長線上，與交于點G，，平分．
(1)求證：；
(2)若，，求的度數．
（10分）25．如圖，在方格紙內將水平向右平移個單位，再向下平移個單位得到.
(1)畫出；
(2)過點畫邊上的垂線；
(3)求圖中的面積.
（10分）26．如圖，，．
(1)試說明；
(2)若，且，求的度數．
參考答案
1．C 2．D 3．B 4．A 5．D 6．C 7．D 8．C 9．B 10．C 11．D 12．B 13．D 14．D 15．A
16．/40度
17．
18．24
19．/50度
20．/度
21．解：設第三根木棒長度為 ，根據題意得：
，即，
∵第三根木棒的長為偶數，
∴可取4，6，8，10，有4種情況．
答：第三根木棒長的取值情況有4種．
22．解：∵AD是BC邊上的高，
∴∠ADB＝∠ADC＝90．
在△ACD中，∠ACB＝180°﹣∠ADC﹣∠CAD＝180°﹣90°﹣20°＝70°．
∵CE平分∠ACB，
∴∠ECB＝∠ACB＝35°．
∵∠AEC是△BEC的外角，，
∴∠AEC＝∠B+∠ECB＝50°+35°＝85°．
答：∠AEC的度數是85°．
23．解：（1）∵∠ACD=∠B+∠BAC，∠B=25°，∠BAC=31°，
∴∠ACD=25°+31°=56°．
（2）∵AD⊥BD，
∴∠D=90°，
∵∠ACD=56°，
CE平分∠ACD，
∴∠ECD=∠ACD=28°，
∴∠AEC=∠ECD+∠D=28°+90°=118°．
24．（1）證明：平分，
，
，
，
．
（2）解：，，
，
平分，
，，
．
25．（1）解：如圖所示，即為所求；
；
（2）解：如圖所示，即為所求；
（3）解：的面積為．
26．（1）證明：∵，
∴，
∴，
∵，
∴，
∴，
即；
（2）解：∵，
∴，
∵，
∴，
∵，
∴．
21世紀教育網(www.21cnjy.com)

展開更多......

收起↑