資源簡介

(共30張PPT)
人教版
數學 八年級
下
第十八章 平行四邊形
18.1.1 第1課時 平行四邊形的邊、角性質
1.理解并掌握平行四邊形的概念及掌握平行四邊形的定
義和對邊相等、對角相等的兩條性質.（重點）
2.根據平行四邊形的性質進行簡單的計算和證明.（難點）
3.經歷“實驗—猜想—驗證—證明”的過程,發展學生的
思維水平.
學習目標
觀察下圖，平行四邊形在生活中無處不在.
情境導入
情境導入
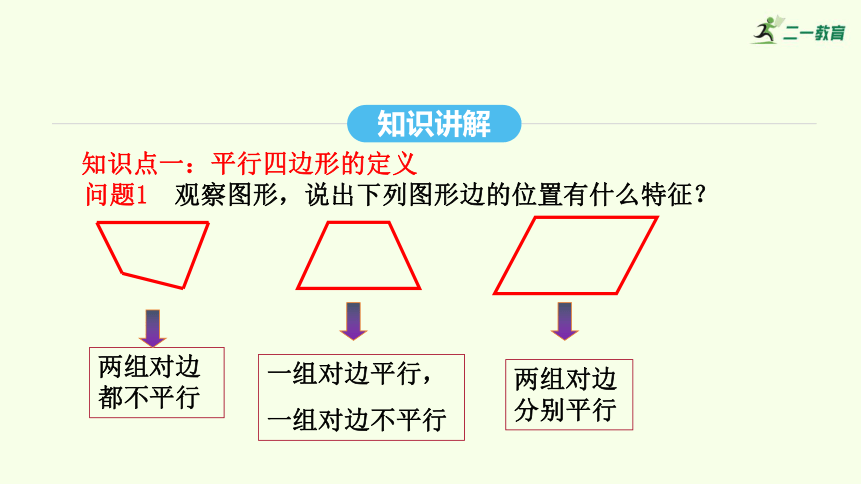
兩組對邊都不平行
一組對邊平行，
一組對邊不平行
兩組對邊分別平行
問題1 觀察圖形，說出下列圖形邊的位置有什么特征？
知識點一：平行四邊形的定義
知識講解
兩組對邊分別平行的四邊形叫做平行四邊形.
2.平行四邊形用“ ” 表示，如圖，平行四邊形ABCD，記作 ABCD ( 要注意字母順序).
1.定義:
A
B
D
C
語言表述：
∵AD∥BC,AB∥DC,
∴四邊形ABCD是平行四邊形.
知識講解
例1 如圖，DC∥GH ∥ AB，DA∥ EF∥ CB，圖中的
平行四邊形有多少個？將它們表示出來.
D
A
B
C
H
G
F
E
K
解：∵DC∥GH ∥ AB，DA∥ EF∥ CB，
∴根據平行四邊形的定義可以判定圖中共有9個平行四邊形，即平行四邊形
AEKG，平行四邊形ABHG, 平行四邊 AEFD, 平行四邊形 GKFD,平行四邊形BEKH, 平行四邊形 CHKF,平行四邊形 BEFC,平行四邊形CDGH,平行四邊形 ABCD.
知識講解
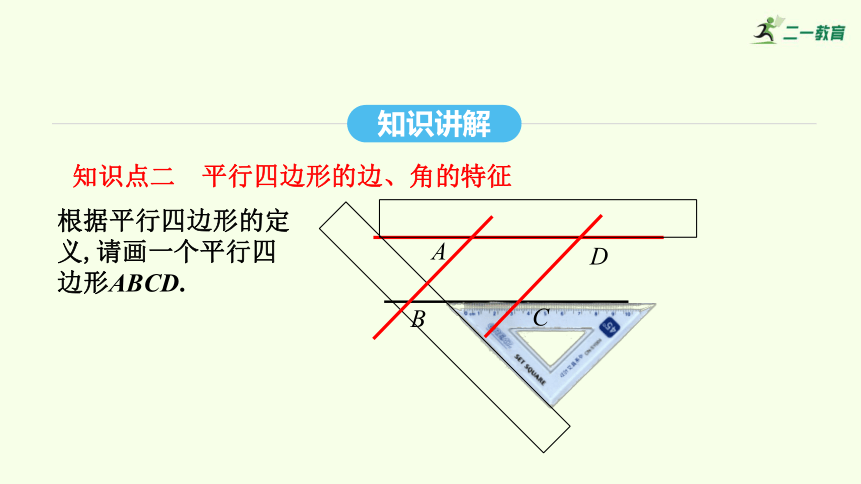
根據平行四邊形的定義,請畫一個平行四邊形ABCD.
D
A
B
C
知識點二 平行四邊形的邊、角的特征
知識講解
A
B
C
D
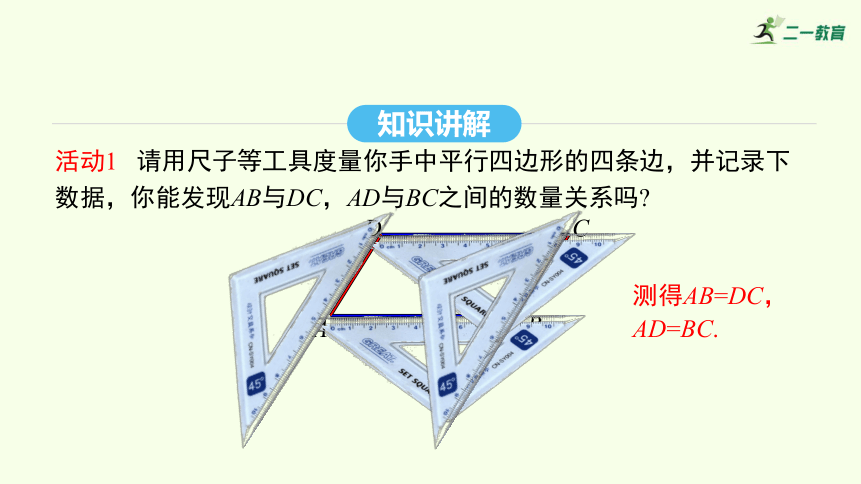
活動1 請用尺子等工具度量你手中平行四邊形的四條邊，并記錄下數據，你能發現AB與DC，AD與BC之間的數量關系嗎
測得AB=DC，AD=BC.
知識講解
A
B
C
D
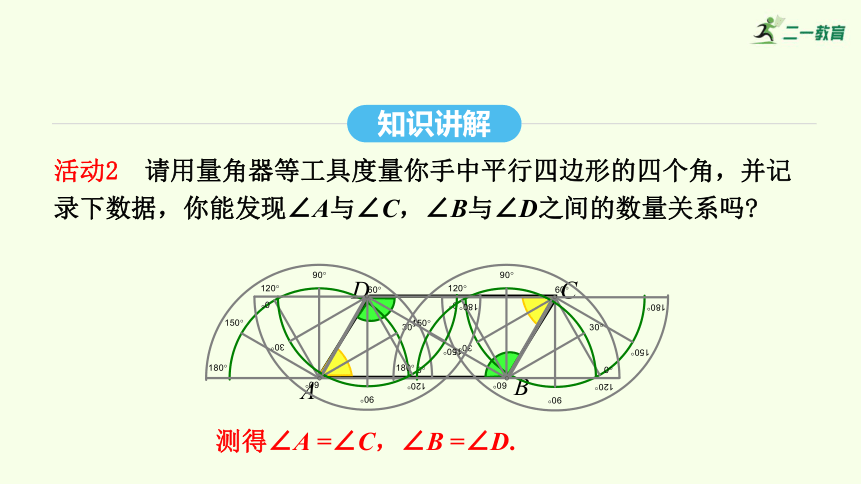
測得∠A =∠C，∠B =∠D.
活動2 請用量角器等工具度量你手中平行四邊形的四個角，并記錄下數據，你能發現∠A與∠C，∠B與∠D之間的數量關系嗎
知識講解
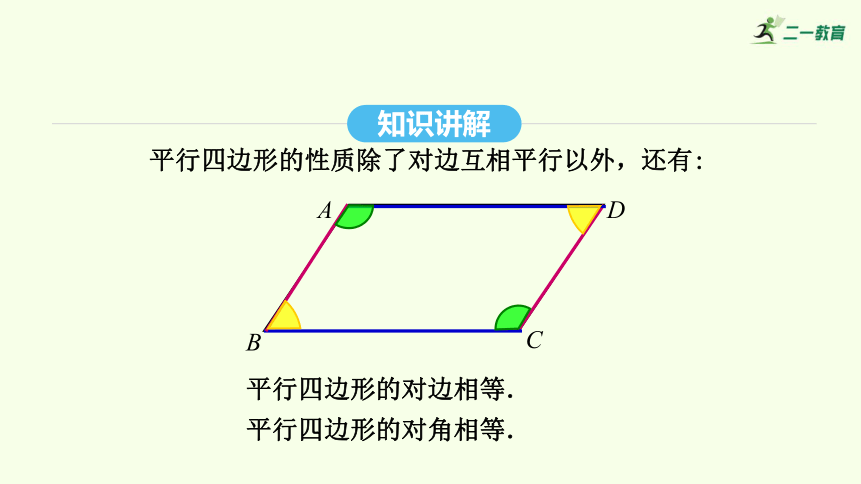
平行四邊形的對邊相等．
平行四邊形的對角相等．
平行四邊形的性質除了對邊互相平行以外，還有:
A
B
C
D
知識講解
思考 不添加輔助線，你能否直接運用平行四邊形的
定義，證明其對角相等？
A
B
C
D
證明：∵四邊形ABCD是平行四邊形,
∴AD∥BC，AB ∥ CD,
∴∠A+∠B=180°，
∠A+∠D=180°，
∴∠B=∠D.
同理可得∠A=∠C.
知識講解
證明：如圖，連接AC.
∵四邊形ABCD是平行四邊形,∴AD∥BC，AB ∥ CD,
∴∠1=∠2，∠3=∠4.又∵AC是△ABC和△CDA的公共邊，∴ △ABC≌△CDA,
∴AD=BC，AB=CD，∠ABC=∠ADC.
∵∠BAD=∠1+∠4，∠BCD=∠2+∠3∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
例1 已知：四邊形ABCD是平行四邊形.
求證:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
知識講解
例2 如圖，在 ABCD中.
(1)若∠A =32。,求其余三個角的度數.
A
B
C
D
∵四邊形ABCD是平行四邊形，
解：
且 ∠A =32。(已知),
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四邊形的對角相等).
又∵AD∥BC（平行四邊形的對邊平行）,
∴ ∠A + ∠B =180。(兩直線平行，同旁內角互補),
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。.
知識講解
(2)連接AC，已知 ABCD的周長等于20cm，AC=7cm，求△ABC的周長.
解：∵四邊形ABCD是平行四邊形(已知),
∴AB=CD，BC=AD(平行四邊形的對邊相等).
又∵AB+BC+CD+AD=20cm(已知),
∴AB+BC= 10cm.
∵AC=7cm,
∴ △ABC的周長為AB+BC+AC= 17cm.
A
B
C
D
知識講解
證明：∵四邊形ABCD是平行四邊形，
∴ AB=CD，AB ∥ CD
∴∠BAE=∠DCF.又∵AE=CF，
∴ △ABE △CDF.∴BE=DF.
例3 如圖，在 ABCD中,E，F是對角線AC上的兩點，并且AE=CF，求證：BE=DF.
A
D
B
C
E
F
知識講解
C
B
F
E
A
D
若m // n，作AB // CD // EF，分別交 m于A、C、E，交n于B、D、F.
m
n
知識點三 平行線間的距離
由平行四邊形的定義易知四邊形ABCD，四邊形CDEF均為平行四邊形.
由平行四邊形的性質得AB=CD=EF.
兩條平行線之間的平行線段相等.
知識講解
若m // n，AB、CD、EF垂直于n，交n于B、D、F，交 m于A、C、E.
B
F
E
A
n
m
C
D
同前面易得AB=CD=EF
點到直線的距離
兩條平行線間的距離：兩條平行線中，一條直線上任意一點到另一條直線的距離
知識講解
例1 如圖，AB∥CD，BC⊥AB，若AB=4cm，S△ABC=12cm2，求△ABD中AB邊上的高．
解：S△ABC = AB BC
= ×4 ×BC=12cm2，
∴BC=6cm.
∵AB∥CD，
∴點D到AB邊的距離等于BC的長度，
∴△ABD中AB邊上的高為6cm．
知識講解
1.在□ABCD中，M是BC延長線上的一點，若∠A=135°，則∠MCD的度數是（ ）
A .45° B.55° C.65° D.75°
A
A
B
C
M
D
隨堂練習
2.判斷題(對的在括號內填“√”，錯的填“×”)：
(1)平行四邊形兩組對邊分別平行且相等. ( )
(2)平行四邊形的四個內角都相等. ( )
(3)平行四邊形的相鄰兩個內角的和等于180°. ( )
(4)如果平行四邊形相鄰兩邊長分別是2cm和3cm，那么周長是10cm. ( )
√
√
√
×
隨堂練習
3.如圖，D、E、F分別在△ABC的邊AB、BC、AC上，且DE∥AC,DF∥BC,EF∥AB，則圖中有_____個平行
四邊形.
第3題圖
3
隨堂練習
證明： ∵四邊形ABCD是平行四邊形，
∴ AB∥CD，AD=BC.∴ ∠CDE= ∠DEA，∠CFB= ∠FBA.又∵DE，BF分別平分
∠ADC，∠ABC,∴∠CDE= ∠ADE，∠CBF= ∠FBA,∴ ∠DEA= ∠ADE，∠CFB=∠CBF,
∴AE=AD, CF=BC,
∴AE= CF.
4.已知在平行四邊形ABCD中，DE平分∠ADC,BF平分∠ABC.求證:AE=CF.
A
B
D
C
E
F
隨堂練習
證明： ∵ 四邊形BEFM是平行四邊形,
∴BM=EF, AB//EF.
∵ AD平分∠BAC,∴∠BAD=∠CAD.
∵AB//EF, ∴ ∠BAD=∠AEF,
∴∠CAD =∠AEF, ∴ AF=EF,
∴ AF=BM.
5.如圖，在 ABC中,AD平分∠BAC,點M,E,F分別是AB,AD,AC上的點,四邊形BEFM是平行四邊形.求證：AF=BM.
B
D
C
E
F
A
M
隨堂練習
6.動手做一做:剪兩張對邊平行的紙條隨意交叉疊放在一起，重合部分構成了一個四邊形，轉動其中一張紙條，線段AD和BC的長度有什么關系？為什么？
A
B
C
D
解：AD和BC的長度相等.
理由如下：由題意知AB//CD,AD//BC，
∴四邊形ABCD是平行四邊形，
∴AD=BC.
隨堂練行
四邊形
定義
兩組對邊分別平行的四邊形
性質
兩組對邊分別平行，相等
兩條平行線間的平行線段相等
兩條平行線間的距離相等
兩組對角分別相等，鄰角互補
平行線間的距離
課后小結
謝謝觀看
https://www.21cnjy.com/recruitment/home/fine

展開更多......

收起↑