資源簡介

(共33張PPT)
第六章 圓周運動
6.4 專題 豎直面內的圓周運動
情景一：過山車
課堂引入：
情景二：水流星
物體在豎直面內做的圓周運動是一種典型的變速曲線運動，該類運動常有臨界問題，并伴有“最大”“最小”“剛好”等詞語，常見模型有兩種
1.輕繩+小球模型
2.輕桿+小球模型
課堂引入：
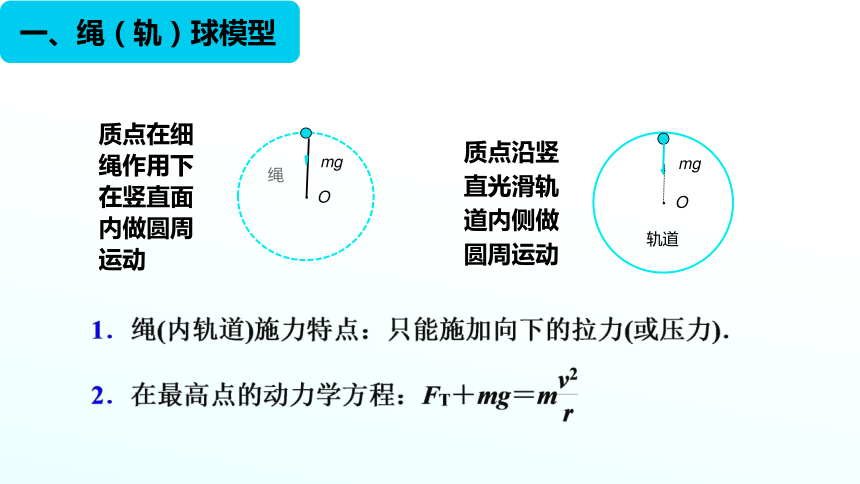
一、繩（軌）球模型
mg
O
繩
mg
O
軌道
質點在細繩作用下在豎直面內做圓周運動
質點沿豎直光滑軌道內側做圓周運動
一、繩（軌）球模型
mg
O
軌道
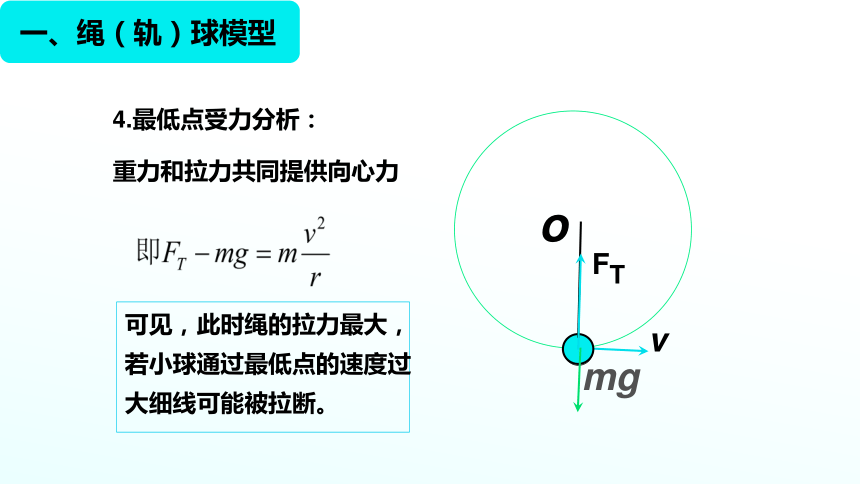
4.最低點受力分析：
重力和拉力共同提供向心力
可見，此時繩的拉力最大，若小球通過最低點的速度過大細線可能被拉斷。
v
o
mg
FT
一、繩（軌）球模型
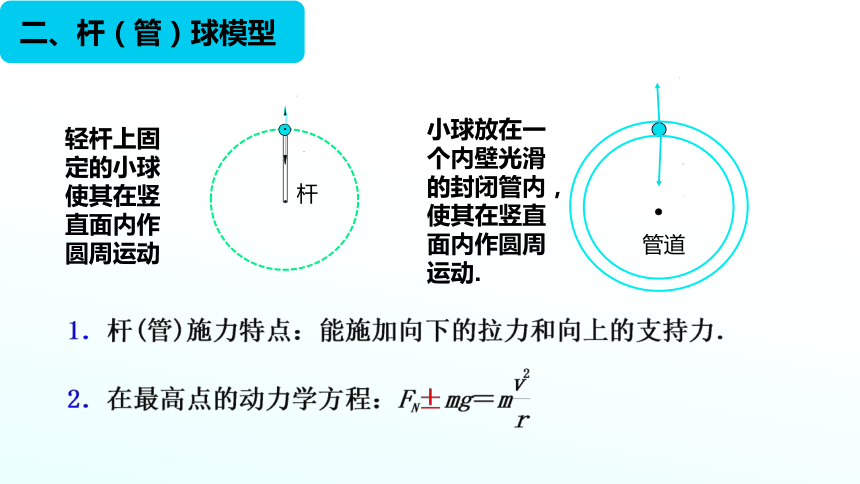
二、桿（管）球模型
mg
O
N
mg
O
N
桿
管道
小球放在一個內壁光滑的封閉管內，使其在豎直面內作圓周運動.
輕桿上固定的小球使其在豎直面內作圓周運動
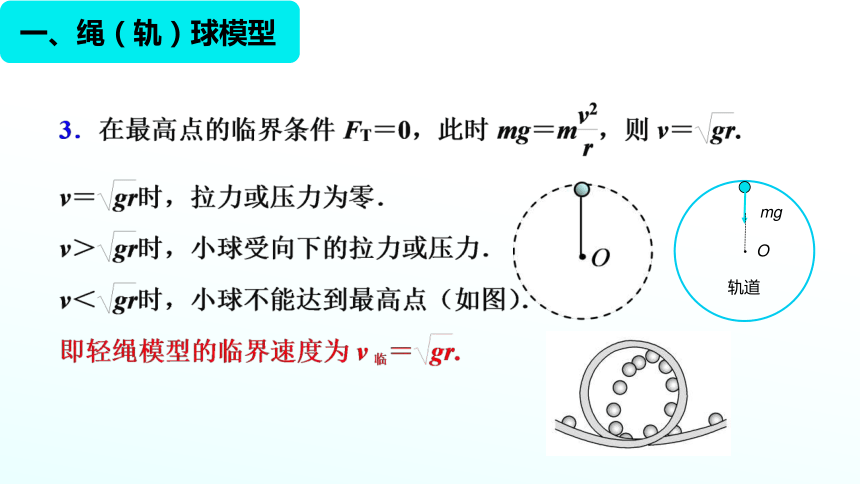
3．最高點的最小速度
FN
mg
o
如圖，由于桿和管在最高處能對小球產生向上的支持力，故小球恰能到達最高點的最小速度v＝0，此時小球受到的支持力FN＝mg.
二、桿（管）球模型
r
FN
mg
二、桿（管）球模型
mg
o
二、桿（管）球模型
r
FN
mg
v
mg
FT
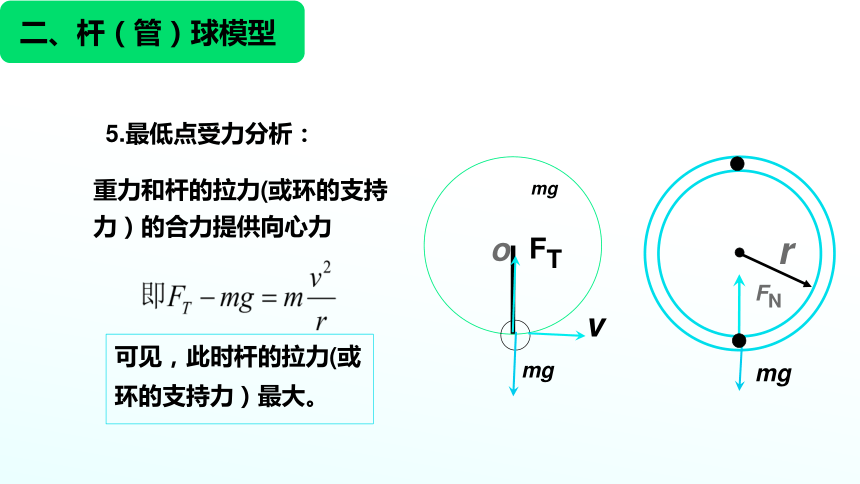
5.最低點受力分析：
重力和桿的拉力(或環的支持力）的合力提供向心力
可見，此時桿的拉力(或環的支持力）最大。
課堂小結
物理情景 最高點無支撐 最高點有支撐
實例 球與繩連接、水流星、沿內軌道運動的“過山車”等 球與桿連接、球在光滑
管道中運動等
圖示
受力 特征 物體受到的彈力方向： 向下或等于零 物體受到的彈力方向：
向下、等于零或向上
課堂小結
課堂小結
1.輕繩（或內軌道）——小球組成無支撐的物理模型（稱為“輕繩模型”）
注：“輕繩”只能對小球產生拉力，不能產生支持力。（內軌道約束類似）
假設質量為m的小球達到最高點時的速度為v,受到繩子的拉力為T，則根據牛頓第二定律，可以得出：
當T=0時，小球再做高點的速度為最小，即：
（1）小球恰好能達到最高點的臨界條件是：
（2）小球恰好能通過最高點的條件是 ， 當 繩子有拉力（軌道對球有壓力）。
（3）當 ，小球還未達到最高點就離開軌道。
只受重力
輕繩和輕桿模型：
2.輕桿（或管道）——小球組成有支撐的物理模型（稱為“輕桿模型”）
注：“輕桿”既能對小球產生拉力，也能產生支持力。（管道約束類似）
球過最高點時，設輕桿對小球產生的彈力FN方向向上。
由牛頓第二定律得：
由此可知：
（1）小球恰好能達到最高點的臨界條件是： 故而V0>0就可以通過最高點。
（2）當 ，FN為支持力，方向豎直向上，且隨著速度增大而減小。
（3）當 ，FN=0
（4）當 ，FN為拉力，方向豎直向下，且隨著速度增大而增大。
彈力的大小與方向隨最高點的速度大小變化而改變
輕繩和輕桿模型：
典例分析
【典例1】如圖所示，乘坐游樂園的翻滾過山車時，質量為m的人隨車在豎直平面內旋轉，下列說法正確的是(　　)
A．過山車在過最高點時人處于倒坐狀態，全靠保險帶拉住，沒有保險帶，人就會掉下來
B．人在最高點時對座位不可能產生大小為mg的壓力
C．人在最低點時對座位的壓力等于mg
D．人在最低點時對座位的壓力大于mg
D
典例分析
CD
典例分析
【典例3】如圖，有一個半徑為R的圓弧形軌道，滑塊A、B分別從軌道上面和下面沿軌道滑動，如果要求它們在最高點處不離開軌道，對它們在最高點的速率有什么限制？
典例分析
【典例4】一細繩與水桶相連，水桶中裝有水，水桶與細繩一起在豎直平面內做圓周運動，如圖所示，水的質量m＝0.5 kg，水的重心到轉軸的距離l＝50 cm.(g取10 m/s2)
(1)若在最高點水不流出來，求桶的最小速率；(結果保留三位有效數字)
(2)若在最高點水桶的速率v＝3 m/s，求水對桶底的壓力大小．
典例分析
【答案】　(1)56 N　(2)4 rad/s
典例分析
C
物理學并不是自然界本身，是人類與自然界的對話。
——普利高津
下課！！！！
感謝觀看
Thank you
授課人：XXX

展開更多......

收起↑