資源簡介

(共47張PPT)
1.4 速度變化快慢的描述——加速度
討論
如何比較速度變化大小？
如何比較速度變化快慢？
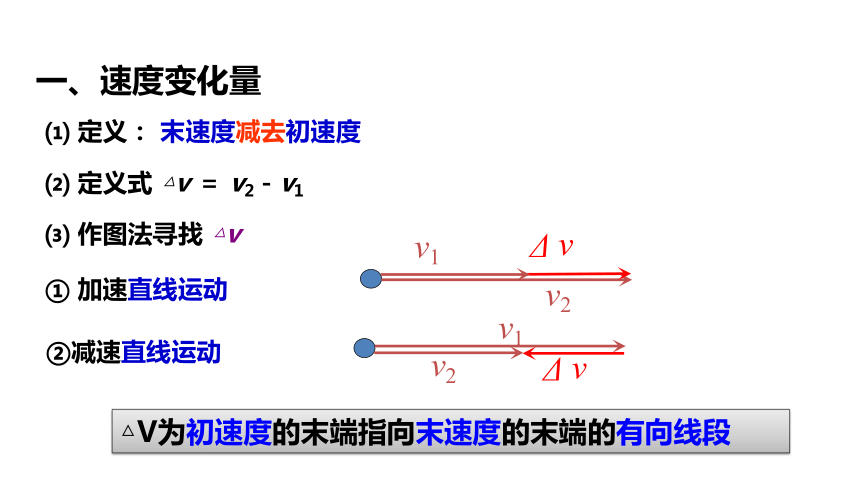
一、速度變化量
⑴ 定義： 末速度減去初速度
⑵ 定義式 △v ＝ v2－v1
⑶ 作圖法尋找 △v
v2
Δ
v
v1
v2
① 加速直線運動
②減速直線運動
Δ
v
v1
△V為初速度的末端指向末速度的末端的有向線段
如圖所示，求小球在碰撞過程中，速度的變化量？
3m/s
3m/s
正方向
1. 確定正方向
2. 將速度表示出來
3. 速度的變化量等于末速度減初速度
即Δv=v2-v1 =－3m/s－3m/s=－6m/s
v1 =3m/s，
v2=－3m/s，
學以致用
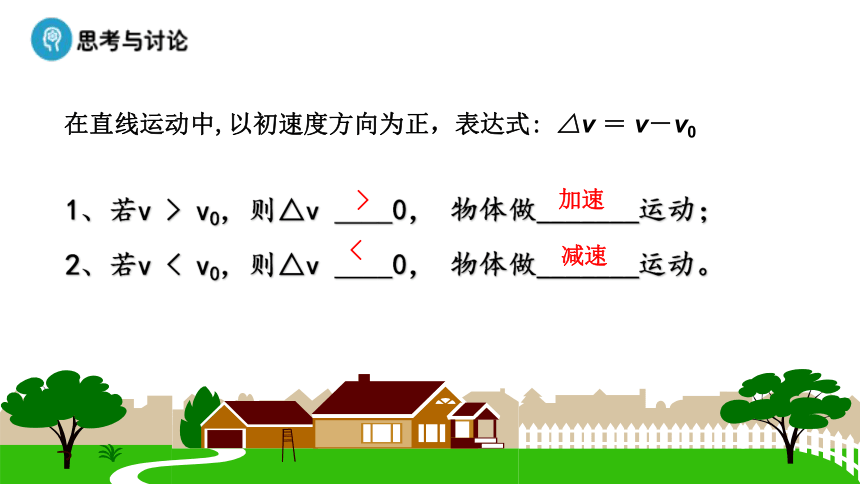
1、若v > v0，則△v ____0， 物體做_______運動；
2、若v < v0，則△v ____0， 物體做_______運動。
在直線運動中,以初速度方向為正，表達式: △v ＝ v－v0
>
<
加速
減速
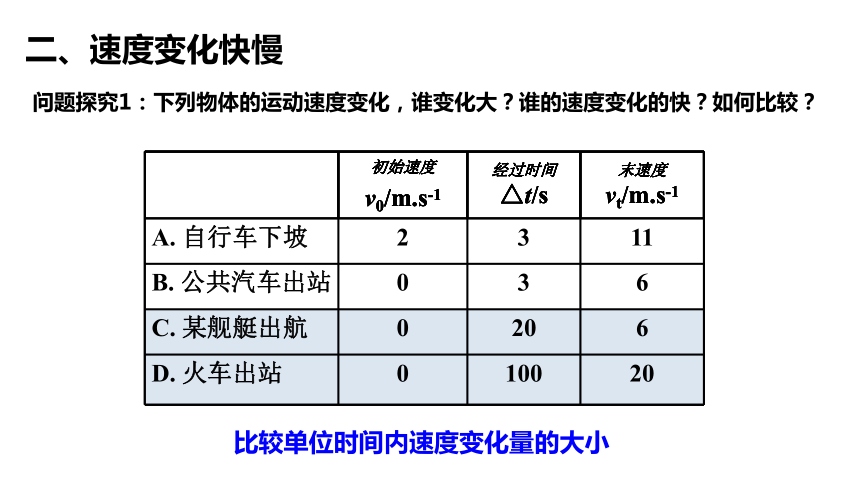
二、速度變化快慢
初始速度 v0/m.s-1 經過時間△t/s 末速度vt/m.s-1
A. 自行車下坡 2 3 11
B. 公共汽車出站 0 3 6
C. 某艦艇出航 0 20 6
D. 火車出站 0 100 20
問題探究1：下列物體的運動速度變化，誰變化大？誰的速度變化的快？如何比較？
比較單位時間內速度變化量的大小
初始速度 v0/m.s-1 經過時間△t/s 末速度vt/m.s-1
A. 自行車下坡 2 3 11
B. 公共汽車出站 0 3 6
C. 某艦艇出航 0 20 6
D. 火車出站 0 100 20
初始速度 v0/m.s-1 經過時間△t/s 末速度vt/m.s-1
A. 自行車下坡 2 3 11
B. 公共汽車出站 0 3 6
C. 某艦艇出航 0 20 6
D. 火車出站 0 100 20
初始速度 v0/m.s-1 經過時間△t/s 末速度vt/m.s-1
A. 自行車下坡 2 3 11
B. 公共汽車出站 0 3 6
C. 某艦艇出航 0 20 6
D. 火車出站 0 100 20
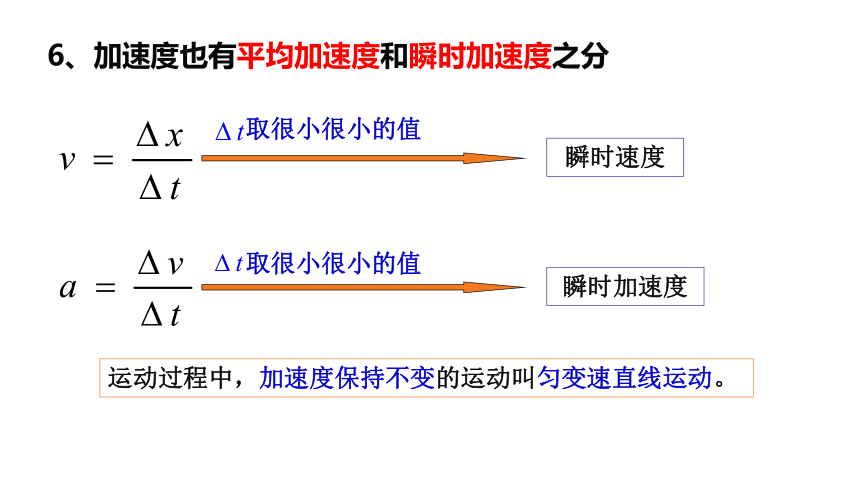
二、加速度
1、定義：
速度變化量和發生這一變化所用時間的比值叫加速度。
2、定義式：
速度變化率
開始時刻物體的速度－初速度
經過一段時間時的速度－末速度
發生速度改變所用時間
二、加速度
3、物理意義：
用于描述物體速度變化快慢的物理量。
4、單位：
米/秒2 （m/s2或m.s-2）
讀作：
“米每二次方秒”
5、矢量性： 加速度方向與速度變化量的方向相同
瞬時速度
瞬時加速度
運動過程中，加速度保持不變的運動叫勻變速直線運動。
取很小很小的值
取很小很小的值
6、加速度也有平均加速度和瞬時加速度之分
【判一判】
A. 速度越大，加速度越大
B. 速度變化越大，加速度越大
C. 速度變化越快，加速度越大
D. 速度越大，而加速度可能越小
E. 速度越小，而加速度可能越大
×
×
√
√
√
結論：加速度與速度、速度變化量沒有必然聯系。
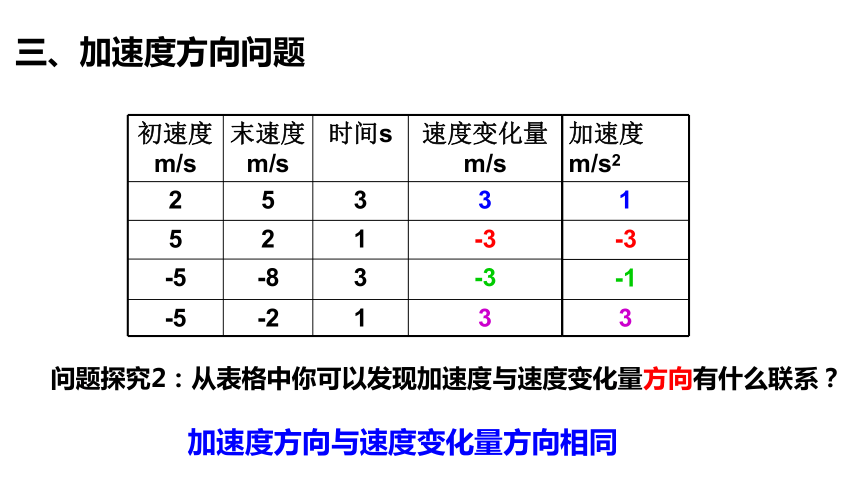
三、加速度方向問題
加速度方向與速度變化量方向相同
初速度m/s 末速度m/s 時間s 速度變化量m/s
2 5 3 3
5 2 1 -3
-5 -8 3 -3
-5 -2 1 3
加速度m/s2
1
-3
-1
3
問題探究2：從表格中你可以發現加速度與速度變化量方向有什么聯系？
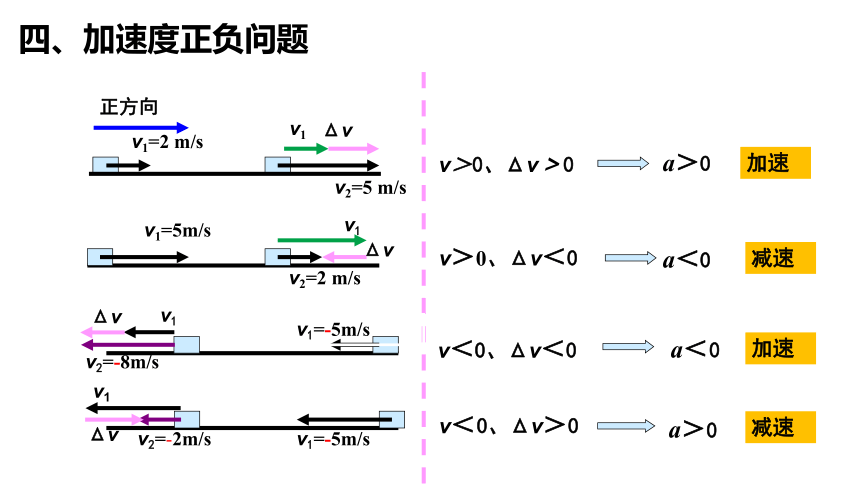
四、加速度正負問題
v2=-2m/s
v1=2 m/s
v2=-8m/s
v1
Δv
v＞0、Δv＞0
v1=5m/s
v1
v2=2 m/s
v1
Δv
正方向
v＞0、Δv＜0
a＞0
a＜0
v1
v1=-5m/s
v2=5 m/s
Δv
v1=-5m/s
Δv
v＜0、Δv＜0
v＜ 0、Δv＞0
a＜ 0
a＞0
加速
減速
加速
減速
v1
v2
Δ
v
v1
v2
a
a
物體作直線運動：
當加速度與初速度方向相同時，物體做加速運動。
當加速度與初速度方向相反時，物體做減速運動。
①加速直線運動
△v
②減速直線運動
t/s
1
0
2
3
4
5
6
t/s
1
0
2
3
4
5
6
0
4
10
8
11
20
12
16
10
9
a1=a2=4 m/s2
a4=1 m/s2
a3=2 m/s2
a1=a2=-4 m/s2
a3=-2 m/s2
a4=-1 m/s2
同向加速
反向減速
a減小v增加慢
a增大v增加快
a減小v減小慢
a增大v減小快
問題探究3：加速度在減小，而速度在增大，有可能嗎？
加速度在增大，而速度在減小，有可能嗎？
m/s
m/s
加速度減小的加速直線運動
加速度增大的加速直線運動
加速度增大的減速直線運動
加速度減小的減速直線運動
有以下幾種情境，請根據所學知識判斷，下列分析和判斷正確的是(　　)
A．火箭剛點火時還沒運動，所以加速度一定為0
B．轎車緊急剎車時速度變化很快，所以加速度很大
C．高速行駛的磁懸浮列車速度很大，所以加速度也一定很大
D．汽車在十字路口右轉，速度的大小不變，加速度為0
答案　B　
當堂訓練
一輛汽車正以15m/s的速度做直線運動，因發生緊急情況剎車后經5s停止，求汽車剎車的加速度。
規定初速度方向為正方向。
有：
答：汽車剎車的加速度大小為3m/s2，方向與初速度方向相反。
假定一個量的方向為正方向，所有與之同向的物理量記為正值，反向的記為負值。
（常定初速度方向為正方向）
結果為負值，說明方向與規定的正方向相反。
解：
1、在運算中必須規定正方向，通常以初速度方向為正方向。則與正方向同向的物理量取為正，與正方向相反的物理量取為負。
2、速度變化量Δv=v-v0的運算一定是末速度v減去初速度v0。
（結果該正則正、該負則負）
3、要注意分析加速度的方向及計算結果中的正、負符號的物理意義。
【速度、速度變化量、加速度比較】
單位 m/s m/s m/s2
方向 速度的方向就是物體運動的方向 Δv＝a·Δt，Δv與a的方向相同 a與Δv的方向相同
物理意義 表示物體運動的快慢和方向 表示物體速度變化的大小和方向 表示物體速度變化的快慢和方向
小結：如何判斷直線運動中“加速”或“減速”的情況
1.物體做加速運動還是減速運動，關鍵是看物體的加速度與速度的方向關系，而不是看加速度的大小，加速度的大小只是反映速度變化的快慢。
2. a的正負，只表示加速度的方向與正方向的關系，不表示物體是加速還是減速。
（1）a與v同向（加速直線運動）
a不變，v隨時間均勻增加
a增大，v增加的越來越快
a減小，v增加的越來越慢
（2）a與v反向（減速直線運動）
a不變，v隨時間均勻減小
a增大，v減小的越來越快
a減小，v減小的越來越慢
加速度的求解
某飛機的起飛速度是50m/s，由于其地面平直跑道的限制，要求飛機在8s內離開跑道，求飛機起飛時的平均加速度。
足球以8m/s的速度飛來，運動員把它以12m/s的速度反向踢回，踢球時間為0.2s，求足球在這段時間內的加速度。
加速度的求解
某飛機的起飛速度是50m/s，由于其地面平直跑道的限制，要求飛機在8s內離開跑道，求飛機起飛時的平均加速度。
解：
答：飛機起飛的平均加速度大小為6.25m/s2，方向與運動方向相同。
足球以8m/s的速度飛來，運動員把它以12m/s的速度反向踢回，踢球時間為0.2s，求足球在這段時間內的加速度。
解：規定初速度方向為正方向。
有：
答：足球的加速度大小為100m/s2，方向飛來的方向相反。
1、槍管內的子彈在某一時刻的速度是100 m/s，經過0.0015 s 速度增加到700 m/s。求子彈的加速度？
2、速度為18 m/s的火車，制動后均勻減速15s后停止運動，求火車的加速度？
2.關于速度和加速度的關系，下列說法正確的是( )
A.物體的速度大，加速度就大
B.物體的速度改變量大，加速度就大
C.物體在單位時間內速度變化大，加速度就大
D.物體的速度為零時，加速度必為零
C
當堂測試
V大a不一定大
△V大a不一定大
△V不一定為0
3.下列所描述的運動中，可能的有（ ）
A.速度變化很大，加速度很小
B.速度變化方向為正，加速度方向為負
C.速度變化越來越快，加速度越來越小
D.速度越來越大，加速度越來越小
AD
當堂測試
△v
a= ——
△t
v – v0
= ———
t
△V方向與加速度方向必定相同
加速度方向必定增加
速度與加速度同向加速
警示：加速度的十個不一定
1.物體的速度大，加速度不一定大。
2.物體的速度很小，加速度不一定很小。
3.物體的速度為零，加速度不一定為零。
4.物體的速度變化大，加速度不一定大。
5.負加速度不一定小于正加速度。
6.加速度為負，物體不一定做減速運動。
7.加速度不斷減小，物體的速度不一定減小。
8.加速度不斷增大，物體的速度不一定增大。
9.物體速度大小不變，加速度不一定為零。
10.加速度方向不一定與速度方向在同一直線上。
七.數學知識補充
1.在數學一次函數y＝kx+b所對應的圖像中，用斜率表示圖線傾斜程度大小，公式中的K值即為直線的斜率。
2.斜率的定義：
3.斜率的正負：
（1）若Δy與Δx同號時，即圖線向上傾斜，斜率為正；
（2）若Δy與Δx異號時，即圖線向下傾斜，斜率為負。
x
A
B
y2
y1
x2
x1
Δx
Δy
y
C
D
x
y2
y1
x2
x1
Δx
Δy
y
問題探究2：勻速直線運動里面，x-t圖像的特點？
斜率代表小汽車做直線運動的速度
X/m
400
300
200
100
0
5
10
15
20
t/s
A
B
是一條傾斜的直線
問題探究3：靜止不動的物體，x-t圖像的特點？
平行于t軸的直線
問題探究1：在前面講的小汽車運動中，小汽車的x-t圖像的斜率代表什么？
位移時間圖像
X/m
400
300
200
100
0
5
10
15
20
t/s
甲
作出乙車的x-t圖像，并求各自的斜率
乙
問題探究4：斜率正負代表什么？
斜率為正代表速度為正，斜率為負代表速度為負
0
100
200
300
400
x/m
甲
乙
問題探究5：是否說明甲的速度大于乙的速度？
斜率正負只能說明速度方向的正負，不能用來比較大小
位移時間圖像
X/m
400
300
200
100
0
5
10
15
20
t/s
甲
對比甲、乙、丙兩個物體的x-t圖像，誰的速度大呢？誰的x-t圖像傾斜程度大
乙
問題探究6：如何在x-t圖像中來比較兩物體速度大小？
丙
①通過斜率的大小比較兩物體速度大小；
②通過圖像的傾斜程度來比較，傾斜程度大的速度大。
位移時間圖像
嘗試描述下甲乙兩車的運動情況
乙車從5s末時刻開始沿著正方向做勻速直線運動
縱截距:開始計時時物體距離參考點的距離
橫截距:物體出發時的時刻(延遲:該物體過了幾秒后才出發）
X/m
400
300
200
100
0
5
10
15
20
t/s
甲
乙
0
100
200
300
400
x/m
甲
乙
甲車從距離參考點200m處開始沿著正方向做勻速直線運動
位移時間圖像
幾種常見運動的x-t 圖像
X/m
400
300
200
100
0
5
10
15
20
t/s
嘗試描述下甲、乙、丙三車的運動情況
-100
-200
-300
甲
乙
丙
甲從距離參考點400m處朝著出發點以-20m/s的速度做反向勻速直線運動
-200
-100
0
200
400
甲
位移時間圖像
幾種常見運動的x-t 圖像
X/m
400
300
200
100
0
5
10
15
20
t/s
嘗試描述下甲、乙、丙三車的運動情況
-100
-200
-300
甲
乙
丙
乙從參考點出發，以-15m/s的速度做反向勻速直線運動
-200
-100
0
200
400
乙
位移時間圖像
幾種常見運動的x-t 圖像
X/m
400
300
200
100
0
5
10
15
20
t/s
嘗試描述下甲、乙、丙三車的運動情況
-100
-200
-300
甲
乙
丙
丙從距離參考點200m處朝著出發點，以-20m/s的速度做反向勻速直線運動，
至坐標原點后，繼續以-20m/s的速度做反向勻速直線運動
-200
-100
0
200
400
丙
位移時間圖像
幾種常見運動的x-t 圖像
X/m
400
300
200
100
0
5
10
15
20
t/s
思維拓展：請描述丁的運動情況
-100
-200
-300
丙
丁
問題探究7：如何在x-t圖像中判斷物體的運動方向？
看其x-t圖像斜率正負是否發生變化？
-200
-100
0
200
400
丁
位移時間圖像
例：如右圖所示，甲、乙兩物體的x-t圖像，則（ ）
A、甲、乙兩物體都做勻速直線運動
B、若甲、乙兩物體在同一直線上運動，則他們不可能相遇
C、 時刻甲、乙相遇
D、 時刻甲、乙相遇
t
乙
x
甲
0
AC
表示兩物體相遇的位置和時刻
x-t圖像中的“龜兔賽跑”
x
t
0
3、烏龜在什么時刻悄悄爬過兔子身旁？
4、兔子醒來的時候烏龜在什么地方呢？
5、誰先到達終點？相差多長時間？
2、兔子是從什么時候什么位置開始睡覺？
1、哪個代表兔子，哪個代表烏龜
A
B
C
畫一畫說一說
t
O
v
△v
△t
v1
v2
t1
t2
α
加速度：
斜率：表示直線的傾斜程度。
結論： v-t圖像中直線的斜率表示加速度。
四、從 v-t 圖象看加速度
t/s
O
v/m·s-1
10
15
5
4
6
2
A
B
思考：A、B兩物體哪個的加速度大？
A物體的加速度為 。
B物體的加速度為 。
0.5m/s2
0.2m/s2
V-t 圖像的斜率就是加速度
（三）速度時間（v-t）圖像中速度、加速度方向判斷方法
1.速度的方向：
①速度圖像在t軸上方，速度為正；
②速度圖像在t軸下方，速度為負。
2.加速度方向：
①速度圖像向上傾斜，加速度為正；
②速度圖像向下傾斜，加速度為負。
v(m/s)
4
3
2
1
0
5
10
15
20
t/s
B
C
4、如右圖所示，是某質點運動的v–t圖象，請回答：
(1)質點在圖中各段的過程中做什么性質的運動？
(2)在0～4 s內、8～10 s內、10 s～12 s內質點的加速度各是多少？
解析：(1)質點在0～4 s內做加速直線運動；
4 s～8 s內，質點做勻速直線運動；
8 s～10 s內質點做減速直線運動；
10 s～12 s內質點反向做加速直線運動．
學以致用
5、質點做直線運動的v-t圖象如圖所示，則（ ）
A. 在前2 s內質點的位移逐漸減小
B. 在1～3 s內質點做加速度a＝－2 m/s2的變速直線運動
C. 在2～3 s內質點的運動方向與規定的正方向相反，加速度方向同1～2 s內的加速度方向相同
D. 以上說法均不正確
BC
（四）幾種常見v-t圖像
v
0
t


代表物體沿正方向做v0=0的勻加速直線運動
代表物體沿正方向做勻速直線運動


v
t
v
0
t

④

v
t
代表物體沿正方向做a逐漸增大的加速直線運動
④代表物體沿正方向做a逐漸減小的加速直線運動
（四）幾種常見v-t圖像
⑦物體沿正方向做v0≠0的勻減速直線運動
⑧物體沿負方向做v0=0的勻加速直線運動
v
0
t
⑦
⑧
v0
t
v
甲
0
t0
交點：表示兩物體在此時刻速度相等
t
v
（四）幾種常見v-t圖像
例1：如圖所示為A、B兩質點的v－t圖象．對于A、B兩質點的運動，下列說法中正確的是(　　)
A. 質點A向所選定的正方向運動，質點B與A的運動方向相反
B. 質點A和B的速度并不相同
C. 在相同的時間內，質點A、B的位移相同
D. 不管質點A、B是否從同一地點開始運動，
它們之間的距離一定越來越大
AB
例2：質點做直線運動的v-t圖象如圖所示，則（ ）
A. 在前2 s內質點的位移逐漸減小
B. 在1～3 s內質點做加速度a＝－2 m/s2的變速直線運動
C. 在2～3 s內質點的運動方向與規定的正方向相反，加速度方向同1～2 s內的加速度方向相同
D. 以上說法均不正確
BC

展開更多......

收起↑