資源簡介

專項訓練六　常考解直角三角形模型
類型一　背靠背型
圖形背景一般為銳角三角形,通過在三角形內作高,構造出兩個直角三角形,其中公共邊CD是解題的關鍵.
【等量關系】CD為公共邊,AD+BD=AB.
模型演變
圖1　 　圖2
【等量關系】如圖1,CE=DA,CD=EA,CE+BD=AB;如圖2,CD=EF,CE=DF,AD+CE+BF=AB.
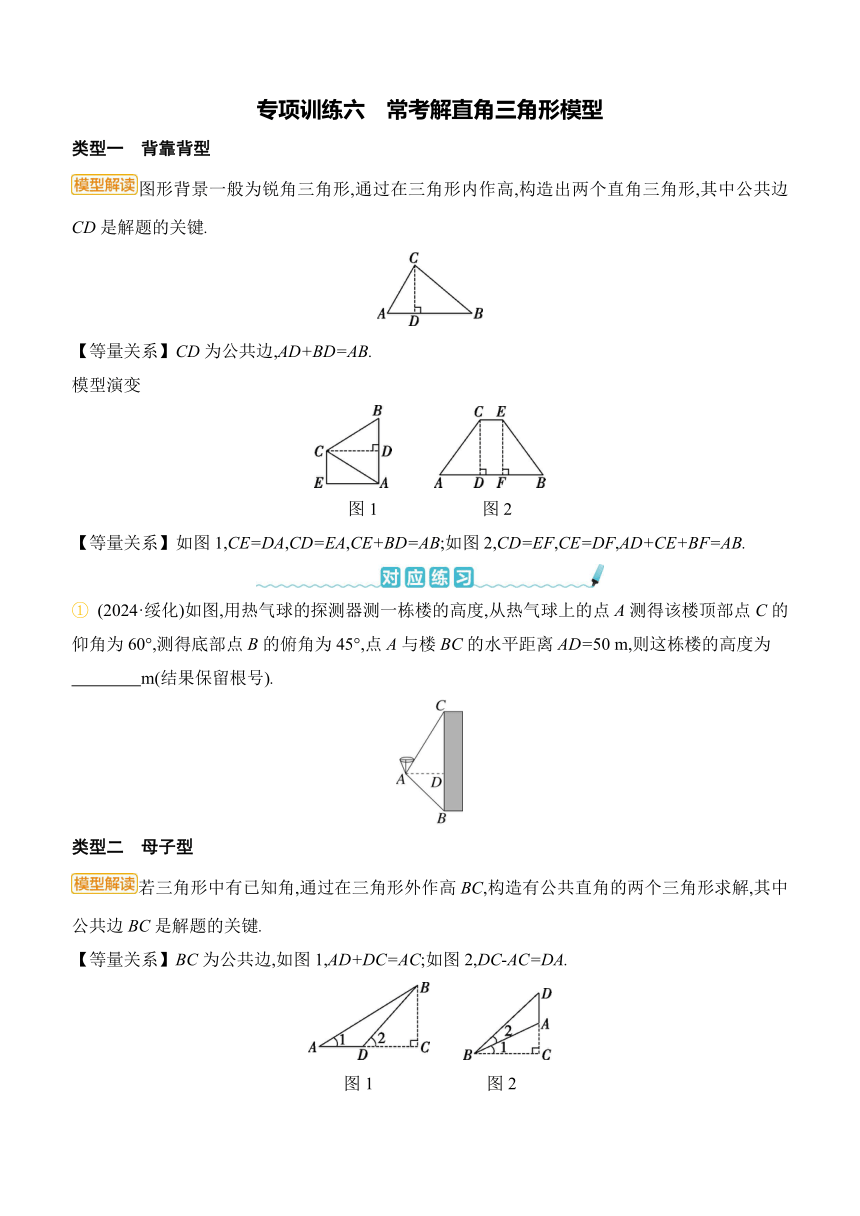
① (2024·綏化)如圖,用熱氣球的探測器測一棟樓的高度,從熱氣球上的點A測得該樓頂部點C的仰角為60°,測得底部點B的俯角為45°,點A與樓BC的水平距離AD=50 m,則這棟樓的高度為
　　　　m(結果保留根號).
類型二　母子型
若三角形中有已知角,通過在三角形外作高BC,構造有公共直角的兩個三角形求解,其中公共邊BC是解題的關鍵.
【等量關系】BC為公共邊,如圖1,AD+DC=AC;如圖2,DC-AC=DA.
圖1　　 圖2
模型演變1
圖3　　 圖4
【等量關系】如圖3,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;如圖4,AF=CE,AC=FE,BC+AF=BE.
模型演變2
圖5　 　圖6　 　圖7
【等量關系】如圖5,BE+EC=BC;如圖6,EC-BC=BE;如圖7,AC=FG,AF=CG,AD+DC=FG,BC+AF =BG.
模型演變3
圖8　　 圖9
【等量關系】如圖8,BC=FG,BF=CG,AC+BF=AG,EF+BC=EG;如圖9,BC=FG,BF=CG,EF+BC= EG,BD+DF=BF,AC+BD+DF=AG.
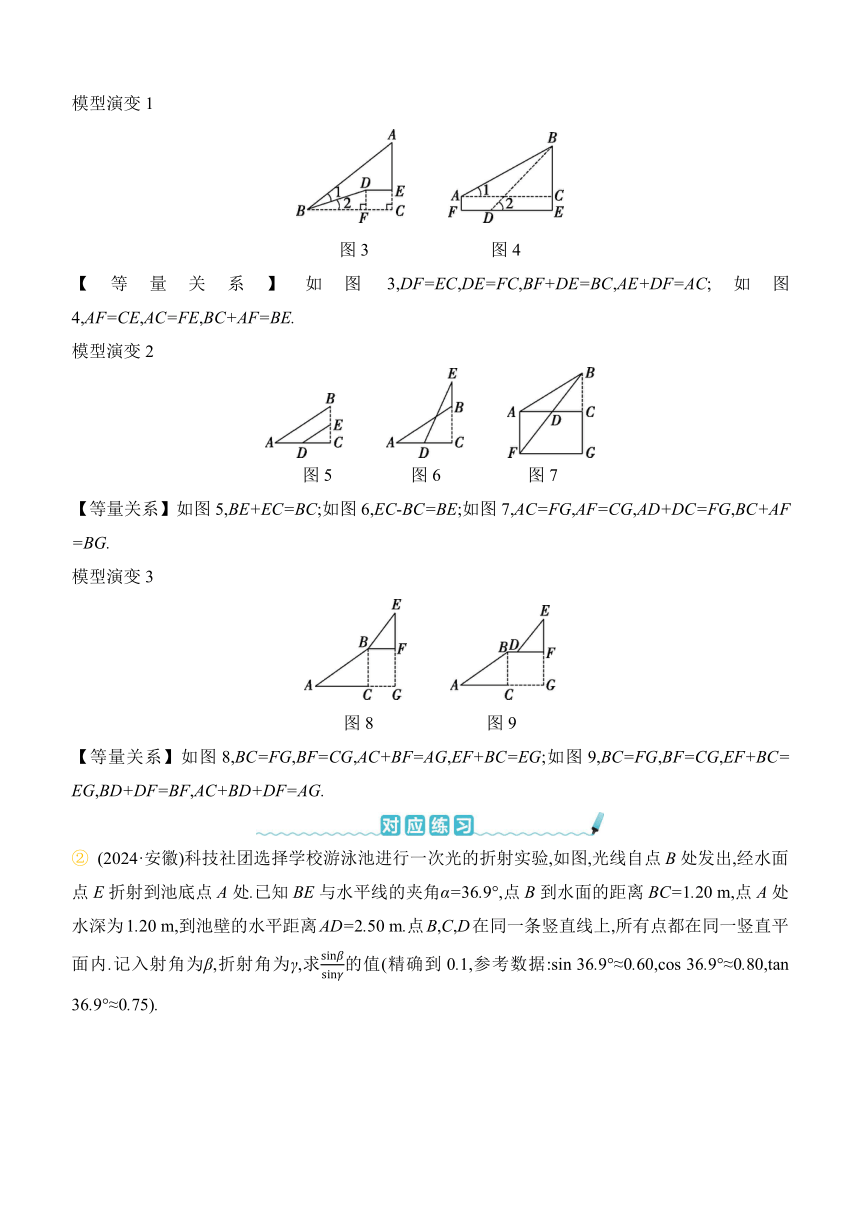
② (2024·安徽)科技社團選擇學校游泳池進行一次光的折射實驗,如圖,光線自點B處發出,經水面點E折射到池底點A處.已知BE與水平線的夾角α=36.9°,點B到水面的距離BC=1.20 m,點A處水深為1.20 m,到池壁的水平距離AD=2.50 m.點B,C,D在同一條豎直線上,所有點都在同一豎直平面內.記入射角為β,折射角為γ,求的值(精確到0.1,參考數據:sin 36.9°≈0.60,cos 36.9°≈0.80,tan 36.9°≈0.75).
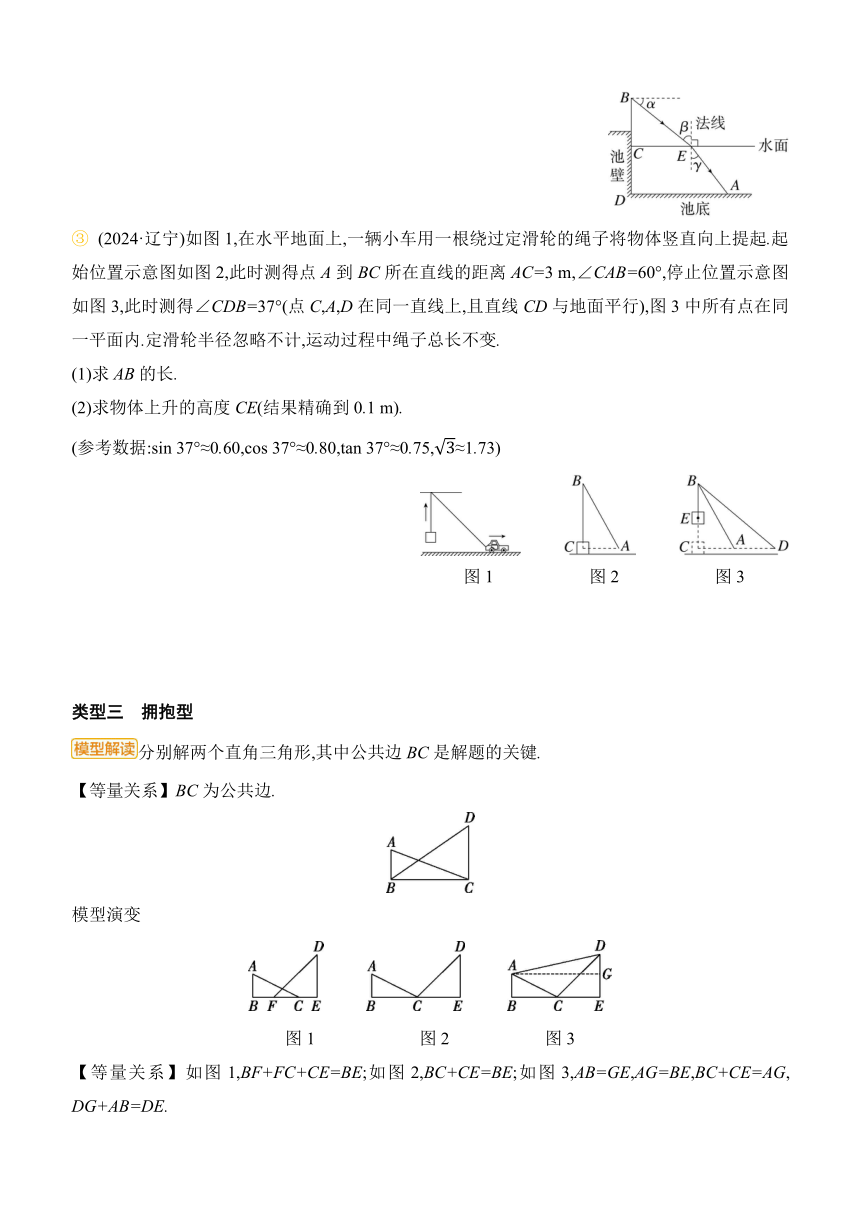
③ (2024·遼寧)如圖1,在水平地面上,一輛小車用一根繞過定滑輪的繩子將物體豎直向上提起.起始位置示意圖如圖2,此時測得點A到BC所在直線的距離AC=3 m,∠CAB=60°,停止位置示意圖如圖3,此時測得∠CDB=37°(點C,A,D在同一直線上,且直線CD與地面平行),圖3中所有點在同一平面內.定滑輪半徑忽略不計,運動過程中繩子總長不變.
(1)求AB的長.
(2)求物體上升的高度CE(結果精確到0.1 m).
(參考數據:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
圖1　 圖2　 圖3
類型三　擁抱型
分別解兩個直角三角形,其中公共邊BC是解題的關鍵.
【等量關系】BC為公共邊.
模型演變
圖1　 圖2 圖3
【等量關系】如圖1,BF+FC+CE=BE;如圖2,BC+CE=BE;如圖3,AB=GE,AG=BE,BC+CE=AG, DG+AB=DE.
④ (2024·巴中)某興趣小組開展了測量電線塔高度的實踐活動.如圖所示,斜坡BE的坡度i=1∶,BE=6 m,在B處測得電線塔CD頂部D的仰角為45°,在E處測得電線塔CD頂部D的仰角為60°.
(1)求點B離水平地面的高度AB.
(2)求電線塔CD的高度(結果保留根號).
【詳解答案】
對應練習
1.(50+50)　解析:由題意,得AD⊥BC,
在Rt△ACD中,∠CAD=60°,AD=50 m,
∴CD=AD·tan 60°=50×=50(m).
在Rt△ABD中,∠BAD=45°,
∴BD=AD·tan 45°=50×1=50(m),
∴BC=BD+CD=(50+50)m,
∴這棟樓的高度為(50+50)m.
2.解:如圖,過點E作EH⊥AD于點H,
由題意可知,∠CEB=α=36.9°,
EH=1.20 m,
∴CE=≈=1.60(m),
∴AH=AD-CE=2.50-1.60=0.90(m),
∴AE===1.50(m),
∴sin γ==0.60.
∵sin β=sin∠CBE==cos∠CEB=cos α≈0.80,
∴≈1.3.
3.解:(1)如題圖2,在Rt△ABC中,AC=3 m,∠CAB=60°,
∴∠ABC=30°,
∴AB=2AC=6 m,
故AB的長為6 m.
(2)在Rt△ABC中,AB=6 m,AC=3 m,
根據勾股定理,得BC=
=3(m).
在Rt△BCD中,∠CDB=37°,
∵sin∠CDB=,即≈0.60,
∴BD≈=8.65(m),
∴CE=BD-BA=8.65-6=2.65≈2.7(m),
故物體上升的高度CE約為2.7 m.
4.解:(1)由題意,得BA⊥AE,
∵斜坡BE的坡度i=1∶,∴.
在Rt△ABE中,tan∠BEA=,
∴∠BEA=30°.
∵BE=6 m,
∴AB=BE=×6=3(m),AE=AB=×3=3(m),
∴點B離水平地面的高度AB為3 m.
(2)如圖,過點B作BF⊥CD,垂足為F.
由題意,得AB=CF=3 m,BF=AC,
設EC=x m,
∵AE=3 m,
∴BF=AC=AE+CE=(x+3)m.
在Rt△CDE中,∠DEC=60°,
∴CD=CE·tan 60°=x(m).
在Rt△BDF中,∠DBF=45°,
∴DF=BF·tan 45°=(x+3)(m).
∵DF+CF=CD,
∴x+3+3=x,
解得x=6+3,
∴CD=x=(6+9)(m),
∴電線塔CD的高度為(6+9)m.

展開更多......

收起↑